Luqman Saleem
- 17
- 3
I have an infinite sheet (in lossless, homogeneous medium) of time-harmonic current in ##yz##-plane at ##x=−d##. The current density on this sheet is given by
$$\mathbf{J}=\hat{z}J_0\delta(x+d)$$
##δ(x+d)## is delta function. Moreover, there is a perfect electric conductor (PEC) half space at ##(0<x<∞,−∞<x,y<∞)## as shown below
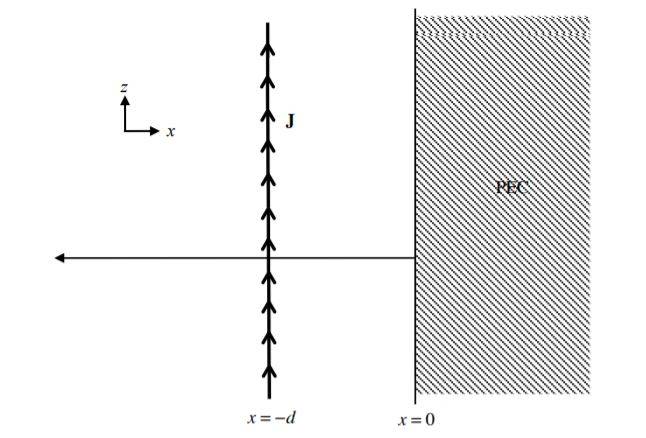
Questions are:
$$\mathbf{J}=\hat{z}J_0\delta(x+d)$$
##δ(x+d)## is delta function. Moreover, there is a perfect electric conductor (PEC) half space at ##(0<x<∞,−∞<x,y<∞)## as shown below
Questions are:
- I want to find fields everywhere in the region
- Electric current density induced on the PEC surface at ##x=0##