- #1
utkarshakash
Gold Member
- 854
- 13
Homework Statement
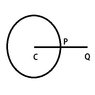
An electron is at P at t=0. It is circulating in anti-clockwise direction with a constant angular speed ω along the shown(see attachment) circular path. Magnetic field at Q (CQ=2R, where R is radius of circle) will be recorded as zero at times ....?
The Attempt at a Solution
The situation is equivalent to a circular ring in which current is flowing in clockwise direction. I can't really see why will the magnetic field be zero at some time. It should be constant as the current does not change.