psy
- 13
- 1
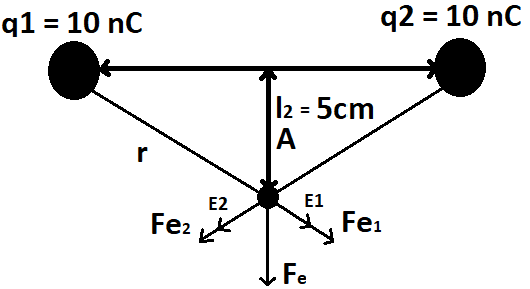
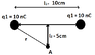
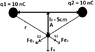
Two positive point charges with a charge of 10nC each are 10cm apart. What is the electric field strength at point A? How is it directed? Which force acts on a charge of 100nC at point A?
 F = k * q1 * q2 / r^2
F = k * q1 * q2 / r^2
E = F/q
r^2 = (l1/2)^2 + (l2)^2 => r = 0,707m
Electric field strength :
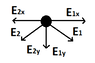
E1 = E2 = 8.99 x 10^9 Nm^2/C^2 * 10*10^-9C / (0,707m)^2 = 179,854 N/C So i "pulled apart" the Electric field strength in x and y components.
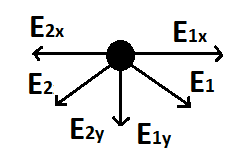
E1y = E1 * cos(45°)= 127,176 N/C
E2y = E2 * cos(45°)=127,176 N/C
E1x = E1 * sin(45°) = 127, 176 N/C
E2x = E2* sin(45°) = 127, 176 N/C
As the Field strength components have the same Amount, yet oppose direction they substract themselvs to Zero, E1y-E2y = 0 ; E1x-E2x = 0. So the Overall Field strength in Point A is Zero.
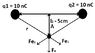
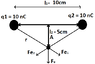
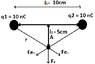
At the second part i suppose to calculate the Electric Force, if at Point A is a Charge q3= 100nC.
Fe1 = k * q1 * q3 / r^2 = 1,7985*10^-5 N
Fe2 = k * q1 * q3 / r^2 = 1,7985*10^-5 N.
The Overall force Fe^2 = Fe1^2 + Fe2 ^2 => Fe = 2,54 * 10^-5.
Is this the right way to calculate it? I am open for every Suggestion.
Kind Regards
E = F/q
r^2 = (l1/2)^2 + (l2)^2 => r = 0,707m
Electric field strength :
E1 = E2 = 8.99 x 10^9 Nm^2/C^2 * 10*10^-9C / (0,707m)^2 = 179,854 N/C So i "pulled apart" the Electric field strength in x and y components.
E1y = E1 * cos(45°)= 127,176 N/C
E2y = E2 * cos(45°)=127,176 N/C
E1x = E1 * sin(45°) = 127, 176 N/C
E2x = E2* sin(45°) = 127, 176 N/C
As the Field strength components have the same Amount, yet oppose direction they substract themselvs to Zero, E1y-E2y = 0 ; E1x-E2x = 0. So the Overall Field strength in Point A is Zero.
At the second part i suppose to calculate the Electric Force, if at Point A is a Charge q3= 100nC.
Fe1 = k * q1 * q3 / r^2 = 1,7985*10^-5 N
Fe2 = k * q1 * q3 / r^2 = 1,7985*10^-5 N.
The Overall force Fe^2 = Fe1^2 + Fe2 ^2 => Fe = 2,54 * 10^-5.
Is this the right way to calculate it? I am open for every Suggestion.
Kind Regards
Attachments
-
 upload_2018-5-6_14-22-25.png2.3 KB · Views: 492
upload_2018-5-6_14-22-25.png2.3 KB · Views: 492 -
 upload_2018-5-6_14-24-54.png2.5 KB · Views: 482
upload_2018-5-6_14-24-54.png2.5 KB · Views: 482 -
 upload_2018-5-6_14-30-48.png3 KB · Views: 490
upload_2018-5-6_14-30-48.png3 KB · Views: 490 -
 upload_2018-5-6_14-36-15.png3.7 KB · Views: 457
upload_2018-5-6_14-36-15.png3.7 KB · Views: 457 -
 upload_2018-5-6_14-36-55.png4.3 KB · Views: 504
upload_2018-5-6_14-36-55.png4.3 KB · Views: 504 -
 upload_2018-5-6_14-39-44.png4.3 KB · Views: 475
upload_2018-5-6_14-39-44.png4.3 KB · Views: 475 -
 upload_2018-5-6_14-55-39.png3.8 KB · Views: 916
upload_2018-5-6_14-55-39.png3.8 KB · Views: 916 -
 upload_2018-5-6_15-39-14.png1.3 KB · Views: 393
upload_2018-5-6_15-39-14.png1.3 KB · Views: 393