Electrostatic force,electric field,electric potential,electric flux

[jasonlewiz]

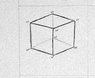
Cube: 10 cm each side

Each q at the corner of the cube is +100 sc.

Find:

a) magnitude and direction of the electrostatic force at the center of the cube.
b) magnitude and direction of the electric field at the center of the cube of tq in place at this pt.
c) find the electric potential and work done if tq of 1000 sc is placed at the center of the cube.
d) what is the electric flux at the center of the cube.


My Solution:

a)

Sq1q9 = square root of (5 cm)^2+(5 cm)^2 = 7.07 cm
S29,S39,S49,S59,S69,S79,S89= 7.07 cm

Fq1q9=k[q1q9/(s19)^2 =1 dyne cm^2/sc^2[(100sc)(100sc)/(7.07cm)^2] = 200.08 dyne
Fq29,Fq39,Fq49,Fq59,Fq69,Fq79,Fq89= 200.08 dyne

x and y components

x axis

Fq19 = -200.08 dyne
Fq29 = 0
Fq39 = 200.08 dyne
Fq49 = 0
Fq59 = 0
Fq69 = 200.08 dyne
Fq79 = 0
Fq89 = -200.08 dyne

y axis


c. V= 1 dyne cm^2/sc^2(100/7.07)x8
V= 113.12 dyne. cm

d. Eq = 800 sc x 1 C/1x10^9 sc = 8x10^-7 C

electric flux = 8x10^-7 C/8.85x10^-12 C^2/Nm^2
electric flux = 90,395.48 Nm^2/C

I can't answer letter a and b because I don't know how will I draw the free bodied diagram of it. I attach a drawing so you can see where I place the charges. I hope you can help me :) thanks

 

[graphene]

Try to imagine the filed at the center due to one of the charges and see if gets canceled due to the field of any other charge.

 

[merryjman]

the wording is wrong, i think. part A must involve a tq, and part B cannot. additionally, you do not want to calculate S19, S29, etc. rather, you want S1C (distance from 1 to center of cube), S2C, etc.

however, as graphene mentioned, this is a very tedious way to solve parts A and B. It is easier to use symmetry arguments.