catie1981
- 45
- 0
[SOLVED] electrostatic force
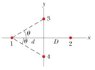
The figure shows an arrangement of four charged particles, with angle θ = 33.0 ˚ and distance d = 3.00 cm. Particle 2 has charge q2 = 8.00 × 10-19 C; particles 3 and 4 have charges q3 = q4 = -1.60 × 10-19 C. What is the distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero?
F= k [(q1*q[2,3,4])/ r^2] (*cos theta, if applicable)
I know that the forces on particle 1 from 2, 3, and 4 are going to cancel...and so I've reached this point
2[9e9(q1*-1.6e-19)/((.03/cos33)^2)cos33]=9e9(q1*8e-19)/((.03+D)^2)
I guess my issue is there are two unknowns in the equation, so I'm stuck. After searching the web, and using the publishers tutorial, I am still utterly lost. The tutorial did ask this very confusing question as well, which I had no idea how to determine the answer for that, soo help would be appreciated for that too. The question was "What multiple of q1 gives the magnitude of the force on particle 1 due to particle (2,3,4)?" The answer was
.000001122312 N/C. WHY??! Any help at this point will be greatly appreciated! Thanks,
Catie
Homework Statement
The figure shows an arrangement of four charged particles, with angle θ = 33.0 ˚ and distance d = 3.00 cm. Particle 2 has charge q2 = 8.00 × 10-19 C; particles 3 and 4 have charges q3 = q4 = -1.60 × 10-19 C. What is the distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero?
Homework Equations
F= k [(q1*q[2,3,4])/ r^2] (*cos theta, if applicable)
The Attempt at a Solution
I know that the forces on particle 1 from 2, 3, and 4 are going to cancel...and so I've reached this point
2[9e9(q1*-1.6e-19)/((.03/cos33)^2)cos33]=9e9(q1*8e-19)/((.03+D)^2)
I guess my issue is there are two unknowns in the equation, so I'm stuck. After searching the web, and using the publishers tutorial, I am still utterly lost. The tutorial did ask this very confusing question as well, which I had no idea how to determine the answer for that, soo help would be appreciated for that too. The question was "What multiple of q1 gives the magnitude of the force on particle 1 due to particle (2,3,4)?" The answer was
.000001122312 N/C. WHY??! Any help at this point will be greatly appreciated! Thanks,
Catie