KiNGGeexD
- 317
- 1
I'm a little stumped with this problem, I have posted a photograph below as there is a diagram to compliment the question
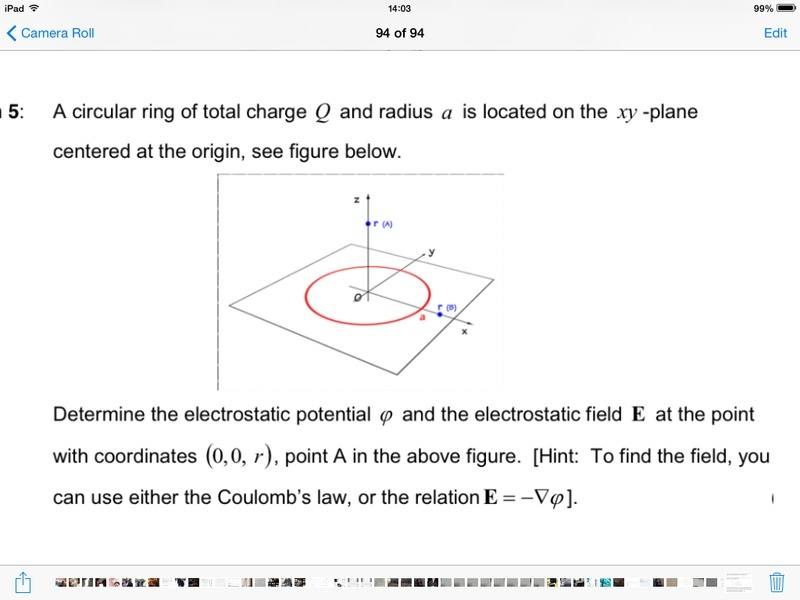 Expressions which I used where
Expressions which I used where
V(r)= k q/r
Where q= σ da
Where da is an element of area
And k= 1/4πεI messed around with these expressions for a while but it didn't really go anywhere I was having trouble defining and element of area (to use spherical coordinates or not).Any help or suggestions would be great thanks in advanced :):):):)
V(r)= k q/r
Where q= σ da
Where da is an element of area
And k= 1/4πεI messed around with these expressions for a while but it didn't really go anywhere I was having trouble defining and element of area (to use spherical coordinates or not).Any help or suggestions would be great thanks in advanced :):):):)