Electrostatics: calculating the E-field of a line charge

[Jayalk97]

Hey guys, could anyone tell me if set up this integral correctly? Thanks in advanced!

 

[kuruman]

Hey guys, could anyone tell me if set up this integral correctly? Thanks in advanced!

No, it is not set up correctly. You should not have a double integral. The element of charge at position z is dq = (q/L)dz. Parameter r is the constant distance to the wire from the point where you want to know the field. You do not integrate over r because you want the field as a function of r.

On Edit: What is the z-component of the position vector of the point of observation P? That should also be made part of the integrand unless you want to calculate the field at the perpendicular bisector, but your drawing does not show that.

 

[Jayalk97]

No, it is not set up correctly. You should not have a double integral. The element of charge at position z is dq = λdz. Parameter r is the constant distance to the wire from the point where you want to know the field. You do not integrate over r.

Yeah I noticed shortly after posting this that I didn't even have the correct amount of integrals for the differentials. Wouldn't that just make the integral (on mobile so I apologize for bad formatting):

1/(4piEr^2)* int(charge density*dz)
over the length of the line?

Don't I have to account for the angle each section of the charge is compared to the selected point?

 

[kuruman]

Don't I have to account for the angle each section of the charge is compared to the selected point?

You do, but first please clarify where point of observation P is, i.e. provide its coordinates.

 

[Jayalk97]

You do, but first please clarify where point of observation P is, i.e. provide its coordinates.

It's an arbitrary point in cylindrical coordinates.

 

[kuruman]

Then its coordinates can be taken as {r, 0, z}. Note that I set θ = 0 because the problem has cylindrical symmetry and the answer should be independent of the azimuthal angle. Also note that you are looking for the field at distance r from the wire on a circle whose plane is parallel to the xy plane at distance z. In other words, you want to end up with $\vec E = E_r(r,z) \hat r +E_z(r,z) \hat z$. You have two components to calculate each of which is a function of $r$ and $z$. This means that you have to do two separate integrals, one for each component, not one double integral. Superposition demands that you add all contributions in the r-direction separately from the contributions in the z-direction. So you have to consider element of charge $dq = (q/L)dz'$ on the wire, find its separate contributions in the r and z directions at P and then add these over the length of the wire. Note my use of variable $z'$ which stands for the position of $dq$ along the wire. It is not to be confused with $z$ which is the z-coordinate of P.

 

[Jayalk97]

Then its coordinates can be taken as {r, 0, z}. Note that I set θ = 0 because the problem has cylindrical symmetry and the answer should be independent of the azimuthal angle. Also note that you are looking for the field at distance r from the wire on a circle whose plane is parallel to the xy plane at distance z. In other words, you want to end up with $\vec E = E_r(r,z) \hat r +E_z(r,z) \hat z$. You have two components to calculate each of which is a function of $r$ and $z$. This means that you have to do two separate integrals, one for each component, not one double integral. Superposition demands that you add all contributions in the r-direction separately from the contributions in the z-direction. So you have to consider element of charge $dq = (q/L)dz'$ on the wire, find its separate contributions in the r and z directions at P and then add these over the length of the wire. Note my use of variable $z'$ which stands for the position of $dq$ along the wire. It is not to be confused with $z$ which is the z-coordinate of P.

My current rendition of the solution looks something like this(going to try my hand at the correct formatting, if this looks gross I'll edit):

$E = 1/(4piε) * \int l_l/(r^2 +z^2) \, dz'$

So from what I gather I;m going to do the integral twice, but with each one modified to isolate the r and z components.
Sorry it took so long to respond, I was in class. So I think I understand what I have to do, but I'm having trouble with how exactly I'd separate the forces. I'd assume I'd take the cosine and sine of the angles for the z and r components respectively right? How could I get the angle as a function of r and z?

 

[kuruman]

m what I gather I;m going to do the integral twice, but with each one modified to isolate the r and z components.

You still don't understand the reasoning behind what you are supposed to do. A picture is worth a thousand words. Let me draw one and I'll get back to you shortly.

How could I get the angle as a function of r and z?

Do you know what SOH-CAH-TOA means?

 

[Jayalk97]

You still don't understand the reasoning behind what you are supposed to do. A picture is worth a thousand words. Let me draw one and I'll get back to you shortly.

Do you know what SOH-CAH-TOA means?

Yes, I guess I should preface this by saying I'm currently doing this for my electromagnetics class as a third year engineering major, so I do have plenty of experience with vector calculus. That being said I probably worded my previous question poorly haha.

In other words, in order to find the separate r and z component contributions in the line charge, I need to multiply the integrand by sine of the r component, and in a separate integral, cosine for the z component, then add them afterwards correct?

 

[kuruman]

In other words, in order to find the separate r and z component contributions in the line charge, I need to multiply the integrated by sine of the r component, and in a separate integral, cosine for the z component, correct?

Correct. I think you understand what to do, but show me the two integrals just to make sure you are on the right track. A new drawing defining the quantities will also be helpful in checking your work.

 

[Jayalk97]

Correct. I think you understand what to do, but show me the two integrals just to make sure you are on the right track. A new drawing defining the quantities will also be helpful in checking your work.

Here. Would this be the correct integral?

 

[kuruman]

Here. Would this be the correct integral?

No. I thought you understood but you did not. Let me make that drawing that I had in mind.

 

[Jayalk97]

No. I thought you understood but you did not. Let me make that drawing that I had in mind.

Alright cool, thanks for the help by the way, I really appreciate it.

 

[kuruman]

Here is the promised picture. Point P is at coordinates {$r$,$0$,$z$} with respect to origin O.

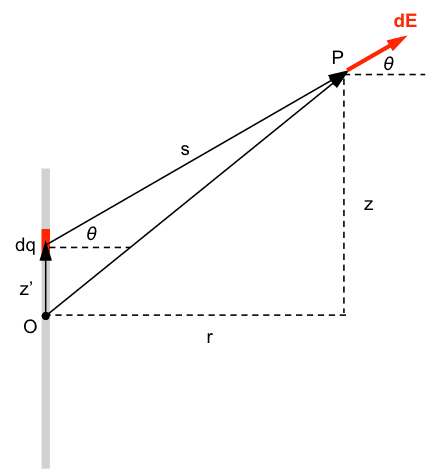
You have element $dq =(q/L)dz'$ on the line at distance $z'$ from the origin. It contributes element $d\vec E$ to the field at P. The distance of $dq$ from P is $s$. Your task is to
1. Find the magnitude of $d\vec E$.
2. Find expressions for the components $dE_r$ and $dE_z$ of $d\vec E$. Express all distances and trig functions in terms of $z$, $z'$, $r$ and $L$.
3. Integrate $dE_r$ and $dE_z$ over the length of the rod.