Electrostatics: Equilibrium distance & Acceleration

[Gazaueli]

Homework Statement

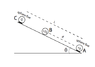
As indicated in the diagram, consider a rail inclined at an angle θ relative to the horizontal axis. A sphere (A) with a charge +q is fixed at the bottom of the rail. A second sphere (B) with a charge +2q and a mass (m) is free to move along the rail. The sphere (C), initially neutral (Q=0) is fixed above the rail, at a distance (L) from the sphere (A).

1. Determine the equilibrium distance (d) between the spheres A and B.

2. What charge, Q, is needed on sphere C in order to move the sphere B upwards with an initial acceleration, a$_{0}$

Homework Equations

Coulombs law: F=$\frac{kq_{1}q_{2}}{r^{2}}$

The Attempt at a Solution

1. It seems like the equilibrium distance would be halfway between spheres A & C, but I think I'm missing something. Because sphere B is mobile, do I need to take into account the force of gravity acting on the sphere?

2. I think that in order to make sphere B move upwards, one would have to place the same charge on C as A, i.e Q$_{C}$=+q, but given that C is placed higher than A, perhaps this changes?

As mentioned in a previous thread, my knowledge of physics is very elementary. Before this class, I had never taken a physics course and the last math course I had was very basic. I need very clear, precise and elementary explications: i.e as you would give to a child, because this is honestly not my strong suit. I don't have a strong mathematical background either, so again, easy, clear explanations (when possible) are best. I apologize if the question is worded rather strangely; it was translated from my homework which is in French, so if something seems unclear, I will do my best to explain it.

 

[LeonhardEu]

1. Initially C is neutral (Q = 0) so in the first question you don't need to consider C. Generally when you want to determine the equillibrium distance you write down all the forces on the body you study and find the point that their sum is zero. Of course take care of the signs.

2. It is actually the same technique as the first only that you use Newtons second law of motion. You write all forces and you proceed. Be careful of the signs!

 

[Gazaueli]

Thank you for responding LeonhardEu!

1. Initially C is neutral (Q = 0) so in the first question you don't need to consider C. Generally when you want to determine the equillibrium distance you write down all the forces on the body you study and find the point that their sum is zero. Of course take care of the signs.

Ok, so since C is initially neutral, I don't need to take it into account for the first problem? So according to that, I would find the $\vec{F}$$_{elec}$ of spheres A and B, ie I used Coulombs law? But after that, I'm not sure how I would find the point that their sum is zero. I wasn't given any real numbers, so I'm not sure how I would go about doing that.

 

[LeonhardEu]

(I suppose from your post that when it says the equilibrium distance it refers to the position where B takes no force). You use coulomb's law to find the electric force from A to B. But on B acts gravity too. So you have the gravitational attraction too. The component of gravity on the vertical axis is equal and opponent to the reaction of the ground so it shouldn't concern you. The thing you need to find is:
(component of gravity parallel to the plane)-(electric force from A to B) = 0. This will give you an equation to solve for distance x. that is the distance from A to point of equilibrium. You don't need real numbers. Just solve it with variables.
As you are new in physics you should know about problem solving these steps:
*Make good figures of the problems
*For each body studied make different diagrams with the body and the forces which act upon it
*NEWTON'S LAWS will give you the solution for accelerations or equilibrium positions (second and first law respectively).
Try to solve it and if you need anything more I'm here

 

[Nickie]

Thank you for your understanding.

1. To determine the equilibrium distance between spheres A and B, we need to consider the forces acting on sphere B. We have two forces acting on sphere B: the electrostatic force from sphere A and the force of gravity. The electrostatic force is given by Coulomb's law: F=\frac{kq_{1}q_{2}}{r^{2}}. The force of gravity is given by F=mg, where m is the mass of sphere B and g is the acceleration due to gravity. In order for the sphere to be in equilibrium, these two forces must be equal and opposite, meaning that F_{electrostatic} = F_{gravity}. This can be written as \frac{kq_{1}q_{2}}{r^{2}} = mg. Solving for r, we get r=\sqrt{\frac{kq_{1}q_{2}}{mg}}. Plugging in the values given in the problem, we get r=\sqrt{\frac{kq(2q)}{mg}}. Therefore, the equilibrium distance between spheres A and B is r=\sqrt{\frac{2kq^{2}}{mg}}.

2. In order to move sphere B upwards, we need to apply a force that is greater than the force of gravity acting on it. This means that the electrostatic force from sphere C must be greater than the force of gravity. Using Coulomb's law, we can calculate the force of electrostatic force between sphere B and sphere C: F=\frac{kq_{1}q_{2}}{r^{2}}. Since sphere B is initially neutral, we can set q_{2}=0. Therefore, F=\frac{kq_{1}Q}{r^{2}}. In order for the force to be greater than the force of gravity, we need to have F>mg. Substituting in the values for F and mg, we get \frac{kq_{1}Q}{r^{2}}>mg. Solving for Q, we get Q>\frac{mgr^{2}}{kq_{1}}. Substituting in the value for r that we found in part 1, we get Q>\frac{2mgkq}{kq_{1}mg}. Simplifying, we get Q>2q. Therefore, in order to move sphere B upwards with an initial acceleration, we need to have a