silkms
- 9
- 0
MENTOR Note: Moved this thread from a math forum hence no template
Is it possible to find this? Really only need the semi major axis or even it's orientation.
In the image below, elements in red are known.
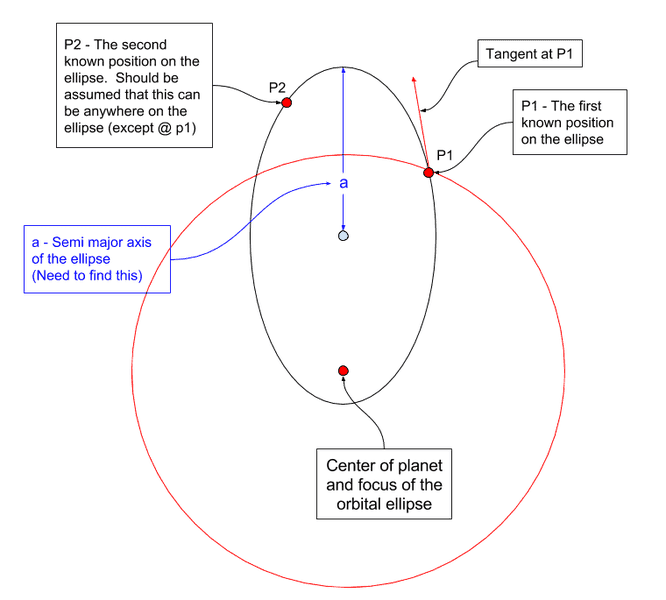
Is it possible to find this? Really only need the semi major axis or even it's orientation.
In the image below, elements in red are known.
Last edited by a moderator: