Elliptic functions, properties of periods, discrete subgroup

[binbagsss]

Homework Statement

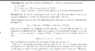
HiI am following this proof attached and am just stuck on the bit that says:

‘since $\Omega$ is a group it follows that $|z-\omega|<2\epsilon$ contains..’Tbh, I have little knowledge on groups , it’s not a subject I have really studied in any of my classes-so the only thing I can think to look to do is look at the defining properties of a group :

Identity exists, inverse exists, closure and associativity

I believe it may be using the ‘converse’ of closure so something like if $a \in \Omega$ and $b$ is not then $a+b$ is not in $\Omega$ ?(not a true converse since it is necessary , not sufficient..but..)

Lastly, if this was the case, there should be a $\epsilon_1$ and a $\epsilon_2$, surely there is nothing to suggest that the discrete points in the set $\Omega$ are equally spaced? (unless ofc, it is a set of periods, which in this case it is, but this hasn’t been derived quite yet, this comes after).I’m probably way off track, but help much appreciated.

Many thanks

Homework Equations

see above

The Attempt at a Solution

see above

 

[fresh_42]

‘since $\Omega$ is a group it follows that $|z-\omega|<2\varepsilon$ contains no element in $\Omega \backslash \{\,\omega\,\}$'

Assume we have a $\nu \in \Omega \backslash \{\,\omega\,\}$ within this ball. Then $\mu := \nu+\omega \in \Omega$ and $|z-\mu|=|(z - \omega ) - \nu | < 2\varepsilon$ in contradiction that there is no such element around $z$.

 

[fresh_42]

... surely there is nothing to suggest that the discrete points in the set $\Omega$ are equally spaced?

So? They are not equally spaced. We have a lattice with a parallelepiped as basis cell, i.e. two side of possibly different lengths. Along one direction they have to be equally spaced, because of the minimality of our choices $\omega_j$. As sums and differences are still elements of $\Omega$, any shorter point would lead to a smaller $\omega_j$.

 

[binbagsss]

and $|z-\mu|=|(z - \omega ) - \nu | < 2\varepsilon$ .

How did you get to this step though , this is the one I am stuck on, which claims to use group properties I think. In the course book, a course In complex arithmetic by jones and singerman, something like that, unfortunately I don't have the book anymore, it is drawn as a diagram , shifting the point in the complex plane, with the same radius, and says by using group properties...

 

[binbagsss]

So? They are not equally spaced. We have a lattice with a parallelepiped as basis cell, i.e. two side of possibly different lengths. Along one direction they have to be equally spaced, because of the minimality of our choices $\omega_j$. As sums and differences are still elements of $\Omega$, any shorter point would lead to a smaller $\omega_j$.

To sound really stupid...how'd you mean only along one direction they have to be equally spaced ? I thought a parallelogram has both sets of parallel lines have the opposite parallel line equal in length .

 

[fresh_42]

How did you get to this step though , this is the one I am stuck on, which claims to use group properties I think. In the course book, a course In complex arithmetic by jones and singerman, something like that, unfortunately I don't have the book anymore, it is drawn as a diagram , shifting the point in the complex plane, with the same radius, and says by using group properties...

To be honest: I scribbled some circles around $z$ and $\omega$, to imagine the situation. All we have here is the triangle inequality. The group property is only used to grant that certain points are still in $\Omega$.

To sound really stupid...how'd you mean only along one direction they have to be equally spaced ? I thought a parallelogram has both sets of parallel lines have the opposite parallel line equal in length .

Sure, but the points are not spread in equal distances, only a square would have: $\omega_1 \perp \omega_2\; , \;|\omega_1| = |\omega_2|$. In general, two diagonal points have a greater distance than two neighbored points, and between the two neighbors, there is also one closer than the other. Only in one direction $\omega_i$ are all points equal hops.

 

[pasmith]

How did you get to this step though , this is the one I am stuck on, which claims to use group properties I think. In the course book, a course In complex arithmetic by jones and singerman, something like that, unfortunately I don't have the book anymore, it is drawn as a diagram , shifting the point in the complex plane, with the same radius, and says by using group properties...

Suppose |z - \omega| &lt; 2\epsilon contains an element \zeta \in \Omega \setminus \{\omega\}.

Then it follows by closure that \zeta - \omega \in \Omega \setminus \{0\}. But by definition |\zeta - \omega| &lt; 2\epsilon, which is a contradiction.

 

[binbagsss]

Suppose |z - \omega| &lt; 2\epsilon contains an element \zeta \in \Omega \setminus \{\omega\}.

Then it follows by closure that \zeta - \omega \in \Omega \setminus \{0\}. But by definition |\zeta - \omega| &lt; 2\epsilon, which is a contradiction.

Ok thanks I understand how to do the step with this arguement.

Why do he notes say ' because it is a group ' though, only discreetness has been used right ?

 

[binbagsss]

To be honest: I scribbled some circles around $z$ and $\omega$, to imagine the situation. All we have here is the triangle inequality. The group property is only used to grant that certain points are still in $\Omega$.

How's would you use the triangle inequality ? I understand the argument used below by contradiction but not sure how you would use the triangle inequality for this ?

Also why do the notes say ' since $\Omega$ is a group ?

Thanks

 

[fresh_42]

How's would you use the triangle inequality ? I understand the argument used below by contradiction but not sure how you would use the triangle inequality for this ?

See post #2.

Also why do the notes say ' since $\Omega$ is a group ?

Thanks

Because we have a sum of two points of $\Omega$ and use that this is again in $\Omega$.

 

[binbagsss]

See post #2.
Because we have a sum of two points of $\Omega$ and use that this is again in $\Omega$.

Mm sorry yes thsnks, I overlooked that since the sum of two periods being a period seems intuitively