Solving Emergency Problem Involving Rod Rotating Around Z Axis

[ShayanJ]

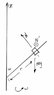
There is a rod rotating around the z axis with angular velocity $\omega$.The angle between the rod and z axis is constant and equal to $\alpha$.A mass m is constrained to move on the rod.The gravitational force is in the negative direction of z axis and the friction between the mass and rod is negligible.At time t=0 , the mass is at distance $r_{0}$ from the origin and is stationary relative to rod.

1-In a proper coordinate system,write the Newton's second law for the mass in a inertial frame of reference and write the differential equations of motion.Highlight the expressions indicating the reaction of rod.

2-Solve the differential equations and write the mass's distance from origin as a function of time.

3-Calculate the reaction force of the rod(direction and magnitude)


thanks

 

[Spinnor]

Does the following get you started?

 

[ShayanJ]

Thanks alot.My mistake was that I didn't write N but only the centripetal force.

But it seems sth is wrong there.Just imagine such a thing not rotating.you know that the mass slides down.So it seems that $N \sin {\alpha}$ is not equal to mg.
Another question.
Last night I worked on it and got some things but there is a big puzzle in my mind.
Textbooks say that the acceleration in spherical coordinates is as following:

$\textbf{a}=(\ddot{r} - r \dot{\phi}^{2} \sin ^ {2} \theta -r \dot{\theta}^{2}) \hat{e_{r}} +$ $( r \ddot{\theta} + 2 \dot{r} \dot{\theta} - r \dot{\phi} ^ {2} \sin {\theta} \cos{\theta}) \hat{e_{\theta}} +$ $(r \ddot{\phi} \sin{\theta} + 2 \dot {r} \dot {\phi} \sin {\theta} + 2 r \dot{\theta} \dot{\phi} \cos{\theta}) \hat{e_{\phi}}$

Shoud I use the r coordinate of the above equation for writing Newton's 2nd law or simply write $m \ddot{r}$ ?
I tried both.When I use the equation above I get crazy things.But when I use $m \ddot{r}$ I get a cosine.
I'm just wondering that the above equation is the most general and can't understand why it becomes wrong in this problem.

The last question.
The $\theta$ coordinate of the acceleration should be zero.But when I write the Newton's 2nd law in that coordinate and replace $\ddot{\theta}$ with zero,I get r=constant,which is clearly wrong.Could you write that?

thanks

 

[pymn_nzr]

Do you know what i said?

 

[asteriatic]

for sharing this problem. I would approach this problem by first understanding the physical setup and identifying the relevant variables and forces at play.

1. Newton's second law states that the net force acting on an object is equal to its mass times its acceleration. In this scenario, the mass m is constrained to move on the rotating rod, so we can write the Newton's second law as:

m\frac{d^2r}{dt^2} = F_{net}

where r is the position of the mass along the rod, t is time, and F_{net} is the net force acting on the mass. In this case, the only forces acting on the mass are the gravitational force (mg) and the reaction force from the rod (R). We can break down the net force into its x, y, and z components as follows:

F_{net,x} = R\cos\alpha - mg\sin\alpha

F_{net,y} = 0

F_{net,z} = R\sin\alpha + mg\cos\alpha

Note that the y component is zero since the mass is constrained to move along the rod, and the frictional force is negligible. Therefore, the differential equations of motion for the mass are:

\frac{d^2r}{dt^2} = \frac{R\cos\alpha - mg\sin\alpha}{m}

\frac{d^2r}{dt^2} = \frac{R\sin\alpha + mg\cos\alpha}{m}

2. To solve these differential equations, we can use the initial conditions given in the problem. At t=0, the mass is at distance r_0 from the origin and is stationary relative to the rod. This means that its initial velocity is zero, so we can write:

\frac{dr}{dt}\bigg|_{t=0} = 0

Integrating this equation with respect to time, we get:

\frac{dr}{dt} = \int_0^t\frac{R\cos\alpha - mg\sin\alpha}{m}dt

\frac{dr}{dt} = \frac{R}{m}\cos\alpha t - \frac{g}{m}\sin\alpha t + C_1

where C_1 is a constant of integration. Using the initial condition, we can solve for C_1: