nchin
- 172
- 0
Energy, Angular Momentum, Torque, solid ball rolling down loop track? help!?
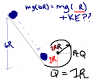
A solid brass ball of mass .280g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 14.0 cm, and the ball has radius r<<R.
(a) What is h if the ball is on the verge of leaving the track when it reaches the top of the loop? If the ball is released at height h = 6.00R, what are the (b) magnitude and (c) direction of the horizontal force component acting on the ball a point Q?
Solution and with diagram on first page, #11.8
www.monmsci.net/~fasano/phys1/Chapter_11_09.pdf
first what does r<<R mean?? is that the same as r<R?
a) so the initial E is mgh when the ball is at the very top.
Ei = Ef
mgh = 1/2mv^2 + 1/2Iω^2 + mg(2R)
So what is mg(2R)?? how can we substitute 2R for h? Also where did 2R come from, the problem never mention anything about 2R.
b) mg(6R) = mg (R) + 1/2mv^2 + 1/2Iω^2
so i understand that the problem states that h = 6R on the left hand side, but why is the right hand side only R (mgR). What does that R mean?
thanks!
A solid brass ball of mass .280g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 14.0 cm, and the ball has radius r<<R.
(a) What is h if the ball is on the verge of leaving the track when it reaches the top of the loop? If the ball is released at height h = 6.00R, what are the (b) magnitude and (c) direction of the horizontal force component acting on the ball a point Q?
Solution and with diagram on first page, #11.8
www.monmsci.net/~fasano/phys1/Chapter_11_09.pdf
first what does r<<R mean?? is that the same as r<R?
a) so the initial E is mgh when the ball is at the very top.
Ei = Ef
mgh = 1/2mv^2 + 1/2Iω^2 + mg(2R)
So what is mg(2R)?? how can we substitute 2R for h? Also where did 2R come from, the problem never mention anything about 2R.
b) mg(6R) = mg (R) + 1/2mv^2 + 1/2Iω^2
so i understand that the problem states that h = 6R on the left hand side, but why is the right hand side only R (mgR). What does that R mean?
thanks!