Uniquebum
- 53
- 1
Question is as follows:
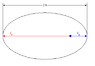
How much energy do i need when i move an object with a mass M from a circular orbit with a radius of R_1 to an ellipse orbit with aphelion radius of R_2.
I'm assuming energy principle is the way to go here but it leads to a question i'd like someone to help me out with.
Do i need to assume the perihelion radius of the new orbit (aphelion radius R_2) is the circular orbit's radius R_1?
Thanks in advance.
How much energy do i need when i move an object with a mass M from a circular orbit with a radius of R_1 to an ellipse orbit with aphelion radius of R_2.
I'm assuming energy principle is the way to go here but it leads to a question i'd like someone to help me out with.
Do i need to assume the perihelion radius of the new orbit (aphelion radius R_2) is the circular orbit's radius R_1?
Thanks in advance.