kulkajinkya
- 12
- 1
I have a quick question. Consider the process S2 to S1 in the figure below
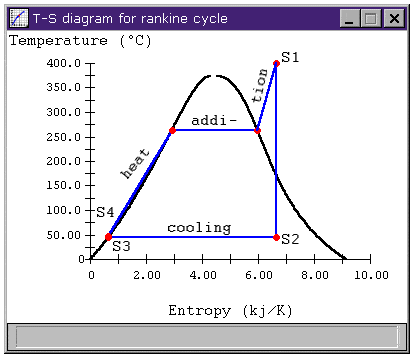
Since this represents wet (isentropic) compression, mathematically we have ΔS=0 (assuming adiabatic compression). But if we consider the process in a physical way, we are going from a region of less disorder (mixture of vapour and water) to a state of more disorder (superheated vapour). Hence physically speaking entropy should increase since we are going to a highly disordered state from a low disorder state. So here is my paradox. How can the process have mathematically 0 change in entropy, but physically it does seem to increase?
Since this represents wet (isentropic) compression, mathematically we have ΔS=0 (assuming adiabatic compression). But if we consider the process in a physical way, we are going from a region of less disorder (mixture of vapour and water) to a state of more disorder (superheated vapour). Hence physically speaking entropy should increase since we are going to a highly disordered state from a low disorder state. So here is my paradox. How can the process have mathematically 0 change in entropy, but physically it does seem to increase?