EOM of simple pendulum submerged in a fluid

[Saptarshi Sarkar]

Homework Statement

Consider a simple pendulum made of a string of length ℓ and a solid metal bob of radius a (a << ℓ). The bob is completely submerged
in the fluid of viscosity η and the pendulum oscillates back and forth in this fluid. If the density of fluid is ρ0 and that of the metal is ρ
then, assuming slow oscillation, show that the equation of motion for the pendulum is given by (slow oscillation makes linear Stoke’s
law viable, that is resistive force due to viscous fluid is given by 6 π η a v, where v is the instantaneous speed of the bob.)

Relevant Equations

$\ddot \theta(t) = -\left(1-\frac{\rho_0}{\rho}\right)\frac gl sin\theta - \frac{9\eta}{2\rho a^2} \dot \theta$

The question :-

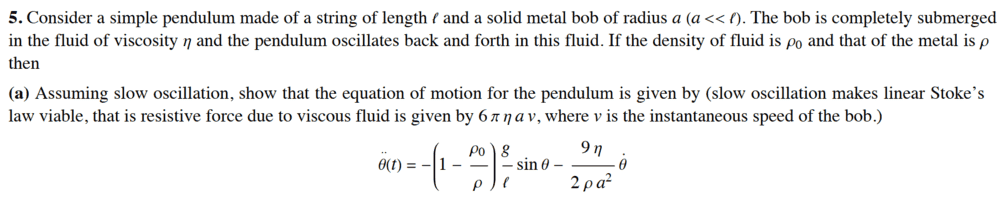
My attempt :-

The confusion that I am having is that to get the required form of the equation of motion, I had to approximate $\theta$ to be small to get $x=l\theta$ so that I could get the acceleration and the velocity. But, I had to leave the $sin(\theta)$ in the equation also. Why shouldn't I use $\theta$ instead of $sin(\theta)$ if I have already used that approximation?

 

[dRic2]

when you write $g sin \theta$ you are evaluating the component of the force along the direction of motion (the tangential component in a circular motion). That direction is not the x direction. So When you write $\frac {d^2 x} {dt^2}$ for the force it's wrong, you should have $\frac {d^2 s} {dt^2}$, where $ds$ is the displacement in the direction of the motion. It's easy to see that $ds = l d \theta$ and from that follow the equation for the tangential velocity and acceleration. You are not making any small angle approximation here, that comes later when you have to deal with $sin \theta$

 

[Saptarshi Sarkar]

when you write $g sin \theta$ you are evaluating the component of the force along the direction of motion (the tangential component in a circular motion). That direction is not the x direction. So When you write $\frac {d^2 x} {dt^2}$ for the force it's wrong, you should have $\frac {d^2 s} {dt^2}$, where $ds$ is the displacement in the direction of the motion. It's easy to see that $ds = l d \theta$ and from that follow the equation for the tangential velocity and acceleration. You are not making any small angle approximation here, that comes later when you have to deal with $sin \theta$

Thanks !