Equilibrium and wire tension problem

[FarazAli]

the problem as in the book
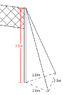
"Two guy wires run from the top of a pole 2.6 m tall that supports a volleyball net. The two wires are anchored to the ground 2.0 m apart and each is 2.0m from the pole. The tension in each wire is 95 N. What is the tension in the net, assumed horizontal and attached at the top of the pole?" - I've attached an image.

What I tried to do was figure out the distance from one wire to the top of the pole.
X = (2.6m^2 + 2.0m^2)^{\frac{1}{2}} = 3.28m

Then using the sum of torques (which is zero in equilibrium) at the first rope as the pivot point
\sum\tau = -\tau_{2} + F_{tensioninnet}X = 0 \Rightarrow F_{tensionnet} = \frac{\tau_{2}}{X} = \frac{95N \cdot 2.0m}{3.28m}

I get 60N, but the answer in the back of the book is 100 Newtons. I also noticed if I multiplied the answer by tan(60) (equilateral triangle at the bottom), and I get 100 N

 

[Doc Al]

No need for distances or torques. Find the net horizontal force exerted by the guy wires on the pole.

 

[FarazAli]

but we don't have a system in only two directions do we?

 

[Doc Al]

but we don't have a system in only two directions do we?

Figure it out in steps. First, find the component in the horizontal plane of the tension from each wire. Then add those two horizontal plane components to find the net force from the wires in the horizontal plane.

 

[FarazAli]

so I resolve the tension into components. You would need an angle to resolve the x-component. We have none. So what I tried was using the law of sines, sin^{-1}\left(\frac{sin 90 \cdot 2.6m}{3.8m}\right) = \theta = 43.2.

So I multiplied the tension times cosine of this to get 65N. So the tension in the net is supposed to be two times this (two guy wires), which is 138N. The answer is 100 N however

 

[Doc Al]

so I resolve the tension into components. You would need an angle to resolve the x-component. We have none. So what I tried was using the law of sines, sin^{-1}\left(\frac{sin 90 \cdot 2.6m}{3.8m}\right) = \theta = 43.2.

You used 3.8m instead of 3.28m.

So I multiplied the tension times cosine of this to get 65N. So the tension in the net is supposed to be two times this (two guy wires), which is 138N. The answer is 100 N however.

These horizontal-plane components are not parallel, so you can't just add them like scalars. Once you get the correct horizontal component, find the angle the two components make and add them like vectors.

Think of the coordinate system this way: the z-axis is vertical (along the pole); the x-axis is parallel to the net; the y-axis perpendicular to the net. The force that each wire exerts on the pole has components along each axis. First find the component of each in the x-y plane (what I've been calling the horizontal plane). Once you've done that, add those two vectors to find the net force in the horizontal plane.