RyanV
- 12
- 0
Homework Statement
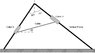
There are two collars hanging on a vertical frame made up of two smooth rods (see attached for figure). If the mass of collar A is 8 kg and the mass of collar B is 4 kg, determine the equilibrium angle \alpha and the tension in the cable between the collars.
Homework Equations
When in equilibrium, \sum F = 0
The Attempt at a Solution
The forces at Collar A,
x: T cos \alpha - Na cos 30 = 0
y: T sin \alpha + Na sin 30 - 8g = 0
The forces at Collar B,
x: -T cos \alpha + Nb sin 45 = 0
y: - T sin \alpha + Nb cos 45 - 4g = 0
where, Na and Nb are forces acting on the beams.
I've simplified the 4 equations to these two equations:
T = 4g / ( cos \alpha - sin \alpha ) ----- (1)
( sin \alpha + cos \alpha tan 30 ) = 2 ------- (2)
( cos \alpha - sin \alpha )
After that, I'm stumped. Any help?
Thanks =)