Sociomath
- 9
- 0
Missing template due to originally being posted in a different forum.
Hi,
I need some guidance on the following problem, please.
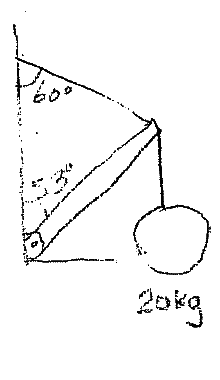
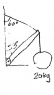
A daredevil attempts to walk the full length of suspended. A 20 kg wrecking ball hangs at the end of this uniform beam of length 4 m and mass 10 kg and is attached to a hinged wall at an angle of 53 degrees. A cable attached to the wall at an angle of 60 degrees is tied to the end of the beam and supports a maximum tension of 525 N.
How far along the beam can a man of 70 kg walk without the cable breaking?
(Apologies for the diagram-sketch.)
##Fgm = (\frac12)(4m)(\sin 37°)+ Fgm(x \cdot 4m)(\sin 37°) - F_{wall}(4m)(\sin 53°)##
##F_w =\displaystyle \frac{29.4889 + 412.8451x}{\sin 53°}##
##F_{net} = F_{wall} - F_t##
##F_{wall}- F_t = 0##
##F_{wall} - 525 N =0##
##F_{wall} = 525 N##
##x = \displaystyle \frac{419.265 - 29.4889}{412.8451} = 0.94412##
Finally, multiply 0.94412 by 4 m:
##0.94412 \cdot 4 = 3.776 m##Thanks in advance.
I need some guidance on the following problem, please.
A daredevil attempts to walk the full length of suspended. A 20 kg wrecking ball hangs at the end of this uniform beam of length 4 m and mass 10 kg and is attached to a hinged wall at an angle of 53 degrees. A cable attached to the wall at an angle of 60 degrees is tied to the end of the beam and supports a maximum tension of 525 N.
How far along the beam can a man of 70 kg walk without the cable breaking?
(Apologies for the diagram-sketch.)
##Fgm = (\frac12)(4m)(\sin 37°)+ Fgm(x \cdot 4m)(\sin 37°) - F_{wall}(4m)(\sin 53°)##
##F_w =\displaystyle \frac{29.4889 + 412.8451x}{\sin 53°}##
##F_{net} = F_{wall} - F_t##
##F_{wall}- F_t = 0##
##F_{wall} - 525 N =0##
##F_{wall} = 525 N##
##x = \displaystyle \frac{419.265 - 29.4889}{412.8451} = 0.94412##
Finally, multiply 0.94412 by 4 m:
##0.94412 \cdot 4 = 3.776 m##Thanks in advance.
Attachments
Last edited: