Equilibrium meter stick problem

[jaymode]

Alright well I have an equilibrium problem to do and I have sat here and stared at it but it does not really seem to make sense or I can't see a way of solving it:
The problem is this(also see attached image):
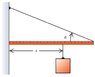
One end of a uniform meter stick is placed against a vertical wall. The other end is held by a lightweight cord that makes an angle theta with the stick. The coefficient of static friction between the end of the meter stick and the wall is 0.360 .

I need to find the maximum value of theta for which the stick well remain in equilibrium; when theta equals 17 degrees, find the minimum value of x for which the stick will remain in equilibrium; and when theta equals 17 degrees, how large must the coefficient of static friction be so that the block can be attached 12.0 cm from the left end of the stick without causing it to slip?

 

[whozum]

Focus on one problem at a time, and make a free body diagram. Theres a downward torque from the block and an upward torque from the string.

 

[jaymode]

Focus on one problem at a time, and make a free body diagram. Theres a downward torque from the block and an upward torque from the string.

I am not given a weight, mass or gravity so I don't see how torque would help me.

The way I see it, the angle that I am trying to find has something to do with the coefficient of friction, and that's all I know.

 

[Gamma]

You may have to assume that the masses are given. Since they did not say that the meter stick is light, you may have to consider it's it weight too.

 

[jaymode]

alright I feel really stupid because I am still having trouble getting it. This is a mastering physics problem and mass is not a variable, or so it says. Maybe I am supposed to eliminate it or something?

 

[Nenad]

I tried soving the first part of the problem. I to torque about the masses connection in order to cancel it out of the calculation. Here is how far I got:

0 = Tsin\theta + \mu T cos\theta - g(m_{Rod} + m_{Box})
0 = Tsin\theta (1-x) - \mu Tcos\theta x + g(0.5m_{Rod})
N = Tcos\theta

here is where I am stuck. For the other parts of the queston, I haven't tried them yet. If you could, write the complete question, all information included.

Regards,

Nenad

 

[jaymode]

I tried soving the first part of the problem. I to torque about the masses connection in order to cancel it out of the calculation. Here is how far I got:

0 = Tsin\theta + \mu T cos\theta - g(m_{Rod} + m_{Box})
0 = Tsin\theta (1-x) - \mu Tcos\theta x + g(0.5m_{Rod})
N = Tcos\theta

here is where I am stuck. For the other parts of the queston, I haven't tried them yet. If you could, write the complete question, all information included.

Regards,

Nenad

That pretty much is the complete question but I will type it out exaclty:
A. What is the maximum value the angle \theta can have if the stick is to remain in equilibrium?

B. Let the angle between the cord and the stick is theta = 17.0 degrees. A block of the same weight as the meter stick is suspended from the stick, as shown, at a distance x from the wall. What is the minimum value of x for which the stick will remain in equilibrium?

C. When theta = 17.0 degrees, how large must the coefficient of static friction be so that the block can be attached 12.0 cm from the left end of the stick without causing it to slip?

And the problem is exactly the same as what was in the first post.

 

[stunner5000pt]

ok since you are not given any NUMBERS you have to make do with ALPHABETS instead. Assume soemthing like this, mass of the block is M, tension of the string is T, and so on. Just think you had numbers but instead just put in the alphabets in the places

for the first part
look at the NET torques exerted by all the components of the system
Assume all forces/torques pointing upward are positive
When calculating the torques of each system use the formula
\tau = rF sin \theta
where theta is the angle between the radius from the center of mass and the force F is acting on it. Since this system is in equilibrium there is no motion, SO the torques wll add up to what?

form the equations from what info i have given to you, thereafter you can address the problems you are given. THink step by step!

 

[Nenad]

ok since you are not given any NUMBERS you have to make do with ALPHABETS instead. Assume soemthing like this, mass of the block is M, tension of the string is T, and so on. Just think you had numbers but instead just put in the alphabets in the places

for the first part
look at the NET torques exerted by all the components of the system
Assume all forces/torques pointing upward are positive
When calculating the torques of each system use the formula
\tau = rF sin \theta
where theta is the angle between the radius from the center of mass and the force F is acting on it. Since this system is in equilibrium there is no motion, SO the torques wll add up to what?

form the equations from what info i have given to you, thereafter you can address the problems you are given. THink step by step!

If you haven't noticed, we alwready got that far. I am trying to solve the first part. Give me some time, I'll have it done.

Regards,

Nenad

 

[Gamma]

For the stick to not to slip, F \leq \mu N ------------(1)

Using Nenad's approach, find F and N and substitue in the above inequality equation. You should get tan \theta \leq ... ----------(2)

or \theta \leq .... This is the max value of theta.

Rest of the problems just follows from equation (2).

Part ii of you question gives you the value of theta and ask for minimum value of x. So substitue for theta= 17 degrees in eq(2) and rearrange to get

x \geq ... ; Also in this part they are saying m(rod) = m (hanging mass). That may simplify your expression.

In part iii , theta and x are given. Substitute them in (2) and rearrange to get mu.


Note: I am a little not clear on the direction of forces at the point where the meter stick touch the wall. I believe Nenad is correct. Frictional force F is along the wall upward direction and the Normal Force N is along the rod to the right.

 

[Nenad]

For the stick to not to slip, F \leq \mu N ------------(1)

Using Nenad's approach, find F and N and substitue in the above inequality equation. You should get tan \theta \leq ... ----------(2)

or \theta \leq .... This is the max value of theta.

Rest of the problems just follows from equation (2).

Part ii of you question gives you the value of theta and ask for minimum value of x. So substitue for theta= 17 degrees in eq(2) and rearrange to get

x \geq ... ; Also in this part they are saying m(rod) = m (hanging mass). That may simplify your expression.

In part iii , theta and x are given. Substitute them in (2) and rearrange to get mu.


Note: I am a little not clear on the direction of forces at the point where the meter stick touch the wall. I believe Nenad is correct. Frictional force F is along the wall upward direction and the Normal Force N is along the rod to the right.

you have the right idea, but its a little tougher than that to prove it. There is probably a step where you have to use the fact that \frac{sin \theta}{cos \theta} = tan \theta.

This is the answer during my lunch break was complicated, it is correct but I don't believe it is the simplest answer; for it uses a lot of variables. There has to ba a way to simplify:

\theta = cos^{-1} (\frac{g(1-x)(m_{Box} + m_{Rod})}{\mu T})

I'm going to keep working on it, the rest of the question is similar, the answers wil be in equation form. Ill keep working on it.

Regards,

Nenad