pinnacleprouk
- 26
- 0
Homework Statement
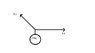
In the attached Diagram, the mass of 2kg is held in a stable equilibrium by two strings acting horizontally and 60 degrees to the horizontal, respectively. Calculate the tension (force) T1 and T2 required to keep the 2kg mass in equilibrium.
The Attempt at a Solution
Resolve forces horizontally
a) T1 Sin 60 = T2 cos 0 = 0.86
Resolve forces vertically
b) (T1 Sin 30 + T2 Sin 90) x 9.81 = 14.715
Substitute a into b
That's as far as I have got, and I don't think what I have done is right!
Any help is appreciated, thanks in advance.