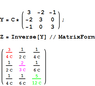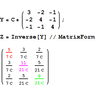Equivalent Capacitance: Find C Between A & B | Tips

[jishnu]

The picture attached with this post shows a combination of capacitors, we are asked to find out the equivalent capacitance between the points A and B.
Provided that all the capacitors are identical and has an individual capacitance C.
Can anyone help me provide basic ideas of solving these kind of problems( I mean a general approach). [emoji4]

 

[Simon Bridge]

A general approach would be to use the kirkoff circuit laws.
If you don't know about those, you had best look for ways to redraw the diagram so it looks simpler.

For instance ... see that box of capacitors in the middle... number the nodes around them 1 through 4, clockwise, from the top left. Label the node closest to A as 0, and the one closest to B as 5.

Notice that node 4 is the same as node 0.

So those first two capacitors are in parallel.

Redraw it like that ... you'll end up with sort-of nested parallel capacitors. You know a rule for parallel capacitors.

The point of these exercizes is to get you to spot these sorts of patterns.

 

[jishnu]

A general approach would be to use the kirkoff circuit laws.
If you don't know about those, you had best look for ways to redraw the diagram so it looks simpler.

For instance ... see that box of capacitors in the middle... number the nodes around them 1 through 4, clockwise, from the top left. Label the node closest to A as 0, and the one closest to B as 5.

Notice that node 4 is the same as node 0.

So those first two capacitors are in parallel.

Redraw it like that ... you'll end up with sort-of nested parallel capacitors. You know a rule for parallel capacitors.

The point of these exercizes is to get you to spot these sorts of patterns.

In that case, I am getting the answer as (2/3) *C
Is that correct..?

 

[cnh1995]

Is that correct

No.

 

[jishnu]

No.

Then could you please help me solve this...

 

[sophiecentaur]

Then could you please help me solve this...

Show us your redrawn diagram as @Simon Bridge recommended - that could be your problem.
Alternatively: We all know how to calculate the equivalent to two series or parallel components but there is also a useful formula for transforming a star of three resistors (or Reactances) to a delta of three equivalent resistors (Reactances) and vice versa.https://www.electronics-tutorials.ws/dccircuits/dcp_10.html You can use that to change your circuit into two deltas which makes the problem easier (visually) and shows up some symmetry which allows you to eliminate some components for the final result. I think that link should help you enough to solve the prob and you will then have another tool in your tool box.

 

[Simon Bridge]

In that case, I am getting the answer as (2/3) *C
Is that correct..?

I don't know: I did not do the problem. Others say "no". Maybe they are correct maybe not.

I cannot help you if you do not explain your reasoning.

 

[jishnu]

A general approach would be to use the kirkoff circuit laws.
If you don't know about those, you had best look for ways to redraw the diagram so it looks simpler.

For instance ... see that box of capacitors in the middle... number the nodes around them 1 through 4, clockwise, from the top left. Label the node closest to A as 0, and the one closest to B as 5.

Notice that node 4 is the same as node 0.

So those first two capacitors are in parallel.

Redraw it like that ... you'll end up with sort-of nested parallel capacitors. You know a rule for parallel capacitors.

The point of these exercizes is to get you to spot these sorts of patterns.

I didn't understand how will the nested arrangement of capacitors looks like... Can u please explain more on that or provide a suitable diagram, the final results that I have posted seems to be wrong to me because I couldn't make any logic out of that, please anyone help me out with this..!

 

[cnh1995]

I didn't understand how will the nested arrangement of capacitors looks like... Can u please explain more on that or provide a suitable diagram, the final results that I have posted seems to be wrong to me because I couldn't make any logic out of that, please anyone help me out with this..!

Put a voltage source between a and b and analyse the diagram. Can you find any series/parallel connection?

 

[jishnu]

Put a voltage source between a and b and analyse the diagram. Can you find any series/parallel connection?

Not exactly. I couldn't figure out one from the diagram the problematic capacitors for me are X and Y(figure 1), but I have doubt whether is it possible to redraw the circuit as to the one I have done in figure 2 then I can find 3 parallel and 1 series circuit of capacitors from that. Am I right in redrawing that circuit? Please explain..

 

[jishnu]

Not exactly. I couldn't figure out one from the diagram the problematic capacitors for me are X and Y(figure 1), but I have doubt whether is it possible to redraw the circuit as to the one I have done in figure 2 then I can find 3 parallel and 1 series circuit of capacitors from that. Am I right in redrawing that circuit? Please explain.. View attachment 226812

Sorry, this is the figure 2 that I have mentioned in my previous post

 

[CWatters]

Fig 2 is not correct. Q and R are not in parallel in the original. You are trying to make too many simplifications in one go. I would start by just combining Y and S (or P and X) and redraw that.

 

[Simon Bridge]

No.

Note... from diagram 1, nodes 2 and 5 are the same.
So Y and S are parallel... you can collapse them to one capacitor between nodes 5 and 3, node 2 vanishes.

Redraw.

Q connects between 1 and 5 while R connects between 4 and 3... so Q and R are NOT parallel.

Take more care.

 

[jishnu]

No.

Note... from diagram 1, nodes 2 and 5 are the same.
So Y and S are parallel... you can collapse them to one capacitor between nodes 5 and 3, node 2 vanishes.

Redraw.

Q connects between 1 and 5 while R connects between 4 and 3... so Q and R are NOT parallel.

Take more care.

Sir, I am having one doubt, if the node 2 collapses then what happens to the connection between node 2 and node 3..?
I want to know whether the newly attached diagram (diagram 3) can be considered correct after collapsing. Can I proceed the same way for the capacitors P and X ?

 

[Simon Bridge]

Last diagram looks good.
The connection between 2 and 3 becomes a connection between 5 and 3.

The key is that wires are part of the node they are attached to. So two nodes joined by a wire are, in fact, the same node.

This let's you simplify the diagram... you are allowed to draw curved lines for wires/connections.

Now see if there are other capacitor pairs you can collapse this way.

 

[jishnu]

Last diagram looks good.
The connection between 2 and 3 becomes a connection between 5 and 3.

The key is that wires are part of the node they are attached to. So two nodes joined by a wire are, in fact, the same node.

This let's you simplify the diagram... you are allowed to draw curved lines for wires/connections.

Now see if there are other capacitor pairs you can collapse this way.

Thank you sir. [emoji4]
I think in that way we can collapse node 4 and combine P and X with parallel connected capacitors formula to achieve even simpler circuit diagram.

 

[jishnu]

Show us your redrawn diagram as @Simon Bridge recommended - that could be your problem.
Alternatively: We all know how to calculate the equivalent to two series or parallel components but there is also a useful formula for transforming a star of three resistors (or Reactances) to a delta of three equivalent resistors (Reactances) and vice versa.https://www.electronics-tutorials.ws/dccircuits/dcp_10.html You can use that to change your circuit into two deltas which makes the problem easier (visually) and shows up some symmetry which allows you to eliminate some components for the final result. I think that link should help you enough to solve the prob and you will then have another tool in your tool box.

Using this conversion I have redrawn my diagram can you please tell me whether its correct or not?
I also want to know can we use resistor combination formulas and wheatstone's bridge concept to deal with reactance(I mean in simplifying and solving them)...!

 

[sophiecentaur]

Using this conversion I have redrawn my diagram can you please tell me whether its correct or not?
I also want to know can we use resistor combination formulas and wheatstone's bridge concept to deal with reactance(I mean in simplifying and solving them)...! View attachment 226863

That looks fine. Now notice that the two parallel capacitors are placed symmetrically across the two paths 0,2,5 and 0,4,5. The PD across them is zero (when all values are equal) because there is no current flowing across, so you now have two pairs of series C in parallel. No sums actually required now!
PS Resistor formulae also apply to Reactances and Impedances (with care of course - big C = small reactance)

 

[jishnu]

I have tried to solve this question in the both ways suggested
1. Collapsing the nodes
2. Using nodal analysis and conversion
But, still I got some problem. Those two ways are giving me different answers to the same problem. Here I am attaching my answers with this post, can anyone please help me to figure out where I went wrong...!
Here I changed the capacitance as
P = Q = R = S = X = Y = "C" (each has same capacitance)

 

[Simon Bridge]

Recheck your working -- especially where you are rearranging the capacitors in method 2. You seem to have a blindness there.
I am getting the same answers by the two methods.

The point of this sort of exercise is to get you to understand how circuits work ... not to find the answer by correctly applying the rules and formulas. The actual answer is irrelevant to the task in front of you.

 

[jishnu]

Recheck your working -- especially where you are rearranging the capacitors in method 2. You seem to have a blindness there.
I am getting the same answers by the two methods.

The point of this sort of exercise is to get you to understand how circuits work ... not to find the answer by correctly applying the rules and formulas. The actual answer is irrelevant to the task in front of you.

I am a bit confused sir, in case of the second method I used the mesh analysis(considering the reactance of the capacitor) to convert the available two stars into delta then as suggested I removed the capacitors connecting 0-2-5 and 0-4-5 (ref post 18) since the PD between them is zero,
There I am stuck with the problem that whether I have to continue solving with reactance(using resistor equations) or by using the new capacitance( using capacitor combination formulas) please help...

 

[jishnu]

Please anybody... Help me out with this problem...[emoji846]

 

[epenguin]

Please anybody... Help me out with this problem...[emoji846]

You appear to be OK in #16. You were probably on the right lines in #3 but then made a mistake. If you had written out your working there you might either have seen the error yourself, or someone could have pointed it out to you.
Go back to #16 - that is quite a simple circuit. It should look even simpler if you put the actual values in (In terms of C).

 

[jishnu]

You appear to be OK in #16. You were probably on the right lines in #3 but then made a mistake. If you had written out your working there you might either have seen the error yourself, or someone could have pointed it out to you.
Go back to #16 - that is quite a simple circuit. It should look even simpler if you put the actual values in (In terms of C).

I have solved the circuit of #16 in #19 by substituting the actual C values, but my confusion is there in the 2nd method(nodal analysis) of #19. Can you please help me figure out where I went wrong from there onwards, because I am getting different answers in those two methods for the same problem.

 

[epenguin]

Sorry I missed that you had given the answer in the left-hand page of #19. I think that is correct, notice it is something that you could have worked out in your head (actually I did). For the other method it is useful to know the right answer beforehand, but I will leave it to those sponsoring this approach.

 

[jishnu]

Sorry I missed that you had given the answer in the left-hand page of #19. I think that is correct, notice it is something that you could have worked out in your head (actually I did). For the other method it is useful to know the right answer beforehand, but I will leave it to those sponsoring this approach.

So, where did I went wrong in the second method..? Please help

 

[The Electrician]

Make the change I show in red and propagate that change through the rest of your calculations:

 

[The Electrician]

In post #19, you say that you're going to do a nodal analysis, but then you give up on that and do a wye-delta conversion.

Do you intend to carry out a nodal analysis?

 

[jishnu]

In post #19, you say that you're going to do a nodal analysis, but then you give up on that and do a wye-delta conversion.

Do you intend to carry out a nodal analysis?

Sorry my mistake, can you please help me know about the difference in nodal analysis and star to delta or vise-versa conversions. Isn't the thing that I have done in #19 also called mesh / nodal analysis(I am not sure about that).

 

[epenguin]

I cannot easily follow everything that you are doing, but for why you are getting a different and wrong answer, it seems to me that you in your second method, maybenot only you, have identified as 'star' something that is not a star. That the 'T' 0124 of #17a is not a star In the textbook sense because 0 and 4 are directly connected with no potential difference between them.

The fault is not in our stars but in ourselves.

 

[The Electrician]

Sorry my mistake, can you please help me know about the difference in nodal analysis and star to delta or vise-versa conversions. Isn't the thing that I have done in #19 also called mesh / nodal analysis(I am not sure about that).

The second thing you did in #19 is called star-delta conversion.

You did not do this: https://www.electronics-tutorials.ws/dccircuits/dcp_6.html, which is called nodal analysis.

 

[The Electrician]

OK. Forget what I said in #27. After you did the Y-Δ transformation: https://en.wikipedia.org/wiki/Y-Δ_transform
each capacitor has a value of C/3. But, you didn't get the schematic after the transformation correct. Two of the capacitors are shorted by a wire that was in the pre-transformation topology as shown here. Look carefully and you'll see that there are 4 capacitors of value C/3 in parallel for a final value of (4C)/3

 

[The Electrician]

Since you have got the correct answer by two methods, I'll show you what I would consider the most general method, which others suggested early on in the thread.

You can do a nodal analysis like this. First select a reference node and number the rest of the nodes like this:

Take the admittance of each capacitor to be just C. Now you can write the admittance matrix Y by inspection using this method:

After you get the admittance matrix, invert it, giving the impedance matrix Z:

The reactance, and hence the inverse of the equivalent capacitance, of each node is equal the value on the main diagonal of the Z matrix.

The value in red, 3/(4 C), is the reactance from node 1 to ground so the equivalent capacitance is (4 C)/3. Similarly, the equivalent capacitance from node 2 to ground is (3 C)/2, and from node 3 to ground it's (12 C)/5. You get all the equivalent capacitances with one matrix calculation.

 

[Babadag]

In my opinion, this could be this way:

Does not it?

 

[Babadag]

It could be this way:

 

[The Electrician]

In my opinion, this could be this way:
View attachment 227162
Does not it?

This is what jishnu did in post #16 and in the left side of the image of post #19

 

[Babadag]

I'm sorry, I just looked at the matrix post!

 

[jishnu]

OK. Forget what I said in #27. After you did the Y-Δ transformation: https://en.wikipedia.org/wiki/Y-Δ_transform
each capacitor has a value of C/3. But, you didn't get the schematic after the transformation correct. Two of the capacitors are shorted by a wire that was in the pre-transformation topology as shown here. Look carefully and you'll see that there are 4 capacitors of value C/3 in parallel for a final value of (4C)/3

View attachment 227136

Thanks allot for the clarification. [emoji4]

 

[The Electrician]

Thanks allot for the clarification. [emoji4]

For extra credit, consider the addition of one more capacitor to the network like this:

Is the equivalent capacitance changed, and if so, what is it?

 

[jishnu]

For extra credit, consider the addition of one more capacitor to the network like this:

View attachment 227191

Is the equivalent capacitance changed, and if so, what is it?

The capacitance would simply become equivalent to "C", is that correct...!

 

[The Electrician]

The capacitance would simply become equivalent to "C", is that correct...!

How did you get that? The extra cap makes it difficult to do parallel/series reduction. But nodal analysis is truly general. Any topology can be solved.

The matrix from post #33 only needs a small tweak to represent the extra capacitor.

Here's the result:

The equivalent capacitance between A and B is (7 C)/5

This shows the power of nodal analysis.

 

[jishnu]

How did you get that? The extra cap makes it difficult to do parallel/series reduction. But nodal analysis is truly general. Any topology can be solved.

The matrix from post #33 only needs a small tweak to represent the extra capacitor.

Here's the result:

View attachment 227194

The equivalent capacitance between A and B is (7 C)/5

This shows the power of nodal analysis.

This is how I got the answer(attached a rough work)
Can you please provide me resources to know more about formation of the admittance matrix, I couldn't understand much relevant things about its matrix formation from the electronics tutorial link that you have provided.

 

[The Electrician]

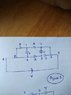
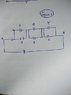
This is how I got the answer(attached a rough work)
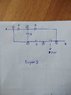
Can you please provide me resources to know more about formation of the admittance matrix, I couldn't understand much relevant things about its matrix formation from the electronics tutorial link that you have provided. View attachment 227195

'

When using the Y-Δ transformation: https://en.wikipedia.org/wiki/Y-Δ_transform

the elements of the circuit must be treated as resistances (impedances in our case), not conductances (admittances in our case). We have taken the capacitances to be admittances because of the way capacitors combine when they are in parallel, and when in series. When capacitors are in parallel, their values are simply added. This is not the way resistors (or inductors) in parallel combine.

So for the purpose of this exercise, we treat the admittance of a capacitor whose value is 2C as if it were an admittance of value 2C, or an impedance of value 1/(2C). If we want the equivalent capacitance of two capacitors 2C and 3C in parallel, it's just 5C. But, if they're in series, we must calculate 1/Ceqv = 1/(2C) + 1/(3C), which gives Ceqv = (6C)/5

For capacitors in series, add their impedances; for capacitors in parallel, add their admittances.

When using the Y-Δ transformation be sure to have the values used in the calculation in impedance form, not admittance form.

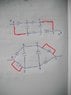
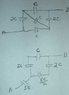
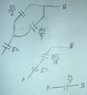
Here are the steps for the solution of the new circuit I gave you using the Y-Δ transformation. In these images the values shown are in admittance form. Even though it's not shown, to use the transformation I took the reciprocals to convert them to impedances before doing the calculations. The results were then converted back to admittance form by taking reciprocals.

Notice how nicely the nodal analysis method with the nodal equations in matrix form took care of all the reductions and algebra automatically.

Regarding more information about the admittance matrix, search on Google for the phrase "admittance matrix by inspection". Also look for "nodal analysis".