Equivalent resistors/capacitors etc. tricky problem

  • Thread starter Thread starter bobthebanana
  • Start date Start date
  • Tags Tags
    Equivalent
AI Thread Summary
The discussion focuses on determining the equivalent capacitance between terminals in a circuit with unclear configurations of resistors and capacitors. The user is confused about which components are in parallel versus series due to a central conductor. Suggestions include visualizing the circuit as a figure-of-eight to clarify the connections. Participants emphasize the importance of identifying potential differences to solve the problem effectively. Understanding the configuration is crucial for applying the correct formulas for equivalent capacitance.
bobthebanana
Messages
21
Reaction score
0

Homework Statement


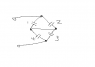
Find equivalent capacitance between terminals

Homework Equations


C_eq = C_1 + C_2 for parallel
C_eq = 1/((1/C_1) + (1/C_2))

The Attempt at a Solution


I can't tell what's in parallel and what's in series. That conductor in the center is throwing me off.

Any help por favor?
You guys might not be able to see the image because it's pending approval. I uploaded it to imageshack:
http://img377.imageshack.us/img377/5690/53235366dg9.png
 

Attachments

  • a.png
    a.png
    966 bytes · Views: 530
Last edited by a moderator:
Physics news on Phys.org
Hi!
party0005.gif

party0006.gif
bobthebanana said:
I can't tell what's in parallel and what's in series. That conductor in the center is throwing me off.

Then pluck it out! :mad:

Hint: Draw it as a figure-of-eight …

does that have the same potentials? :wink:
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Redistribution of Pre-Charged Capacitors
Replies
11
Views
3K
Equivalent capacitance homework problem
2
Replies
67
Views
10K
Equivalent Capacitance: Where to Place the Equivalent Capacitor Between A and B?
Replies
25
Views
4K
What is the Potential Difference Between c and d in This Circuit?
3
Replies
108
Views
11K
Equivalent capacitance in complex circuit
Replies
2
Views
20K
Equivalent capacitance:pentagon shape
Replies
7
Views
3K
Potential Difference of a Capacitor System
Replies
16
Views
8K
Equivalent capacitance of a system from potential difference
Replies
7
Views
7K
Two Capacitors in series for two circuits
Replies
8
Views
1K
Capacitor Charging: Voltmeter, Charge & Voltage Calculations
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top