acadian
- 3
- 0
Hello!
An assignment for my computational modeling course is to demonstrate the use of the Standard Euler method for modeling a simple harmonic oscillator; in this case, a mass attached to the end of a spring.
I have the two coupled first-order differential equations satisfying hookes law: dx/dt = v, and dv/dt = -(k/m)*x
The numerical solutions of which are v(t + dt) = v(t) - k*x(t)*dt / m, and x(t + dt) = x(t) + v(t)*dt to model the velocity and position, respectively.
In a computer program, I've represented this as:
x = x + v*dt;
v = v - k*x*dt / m;
t = t + dt;
with dt = 0.04, m = 1, k = 1, and initial values v = 0, t = 0, and x = 5.
The Purpose of the exercise is to demonstrate how the standard Euler Method is non-stable and results in non-conserved energy.
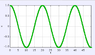
When iterating the above Euler method for sufficiently large periods of time, I've expected x to grow larger after each period but my numerical method above is acting like a conserved-energy Improved Euler method (Euler-cromer)? Please see attached plot.
An assignment for my computational modeling course is to demonstrate the use of the Standard Euler method for modeling a simple harmonic oscillator; in this case, a mass attached to the end of a spring.
I have the two coupled first-order differential equations satisfying hookes law: dx/dt = v, and dv/dt = -(k/m)*x
The numerical solutions of which are v(t + dt) = v(t) - k*x(t)*dt / m, and x(t + dt) = x(t) + v(t)*dt to model the velocity and position, respectively.
In a computer program, I've represented this as:
x = x + v*dt;
v = v - k*x*dt / m;
t = t + dt;
with dt = 0.04, m = 1, k = 1, and initial values v = 0, t = 0, and x = 5.
The Purpose of the exercise is to demonstrate how the standard Euler Method is non-stable and results in non-conserved energy.
When iterating the above Euler method for sufficiently large periods of time, I've expected x to grow larger after each period but my numerical method above is acting like a conserved-energy Improved Euler method (Euler-cromer)? Please see attached plot.
Attachments
Last edited: