Evaluate the definite integral in the given problem

[chwala]

Homework Statement

See attached.

Relevant Equations

Integration by parts.

My interest is on the highlighted part only. Find the problem and solution here.

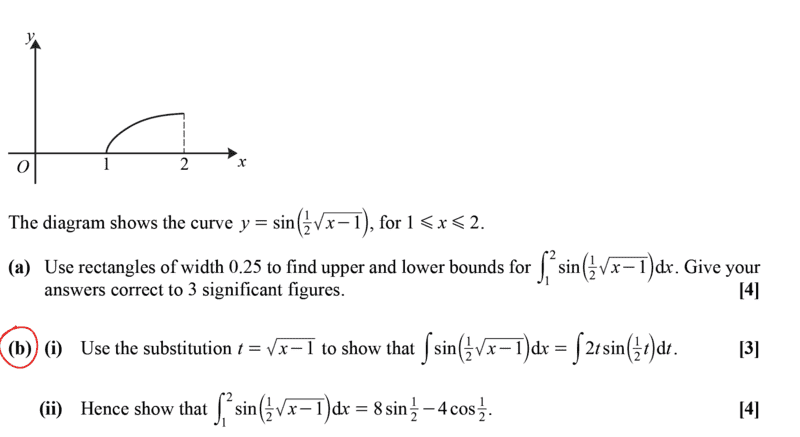
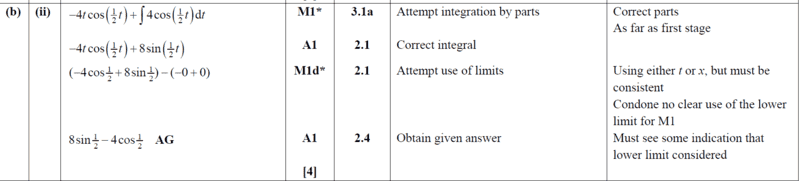
This is clear to me (easy )...i am seeking an alternative way of integrating this...or can we say that integration by parts is the most straightforward way?

The key on solving this using integration by parts is to note that;
$u=t, du=dt, dv=sin \frac {1}{2} t, v=-2 cos \frac {1}{2} t$

 

[anuttarasammyak]

Homework Statement:: See attached.
Relevant Equations:: Integration by parts.

can we say that integration by parts is the most straightforward way?

I am not sure but afraid that we have no better way.