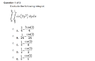Northbysouth
- 241
- 2
Homework Statement
Evaluate the following integral.
I have attached an image of the question.
Homework Equations
The Attempt at a Solution
I know that I need to switch the limits, but I'm not sure how to do this.
Do I just solve y = x/2 for x which would give me:
x = 2y and substitute this in place of the x/2?
Help would be appreciated.