manal950
- 177
- 0
Hi
Evalute the following integers
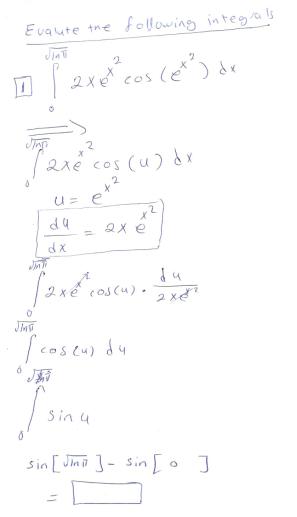
Evalute the following integers
Your substitution is fine.manal950 said:Hi
all is correct instead of substitution ??