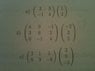mitch_1211
- 95
- 1
I want to express the matrix product Ax as a linear combination of the column vectors in A.
I know for that for (2,3;-1,4)(1;2) i just row reduce the 2 previous matrices and then the solutions give the multiples needed for each column.
How would i go about solving a similar problem but then the matrices are
(2,1,5;6,3,-8)(3;0;-5) the first matrix is 2x3 and the second one is 3x1, i can't augment these and solve for constants can I?
i'm also not entirely sure if the second matrix is x from Ax=b or if it the b matrix, my guess would be that it is the x matrix.
I've tested if the solutions i get multiplied by the appropriate rows of the first matrix gives the second matrix, and it works, but not sure if that was by change or if i am following a valid procedure.
Some explanation on best way to approach these problems would be much appreciated..
I know for that for (2,3;-1,4)(1;2) i just row reduce the 2 previous matrices and then the solutions give the multiples needed for each column.
How would i go about solving a similar problem but then the matrices are
(2,1,5;6,3,-8)(3;0;-5) the first matrix is 2x3 and the second one is 3x1, i can't augment these and solve for constants can I?
i'm also not entirely sure if the second matrix is x from Ax=b or if it the b matrix, my guess would be that it is the x matrix.
I've tested if the solutions i get multiplied by the appropriate rows of the first matrix gives the second matrix, and it works, but not sure if that was by change or if i am following a valid procedure.
Some explanation on best way to approach these problems would be much appreciated..