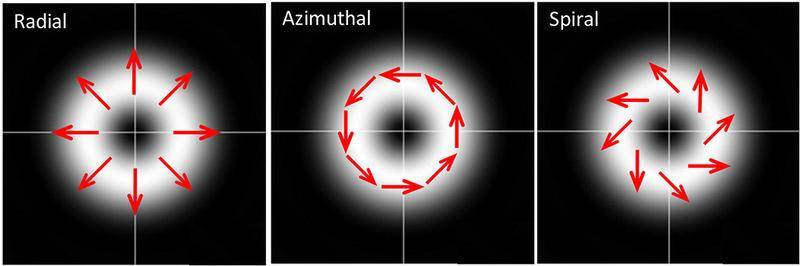
Focusing a radially polarized beam to a single point raises questions about potential destructive interference due to the opposing electric fields. However, while the beam may exhibit a zero at its center due to symmetry, it does not completely cancel out; instead, it produces a diffraction pattern with a bright ring around the center. The resultant energy distribution is influenced by the vector sum of the beam's components, which means total cancellation is unlikely. The limitations of optics ensure that there will always be a finite beam width, preventing a perfect focus. Experimental evidence supports these findings, demonstrating the behavior of focused radially polarized beams.