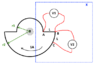
Stefan Gustafsson said:
Lets look at another problem for a second. Answering this should not require much effort.
I can answer two of your questions immediately:
4) What is ∇xE in the region X?
Obviously zero since there is no B field anywhere within X. This of course does not mean
E = 0.
5) Is the E-field in region X conservative or non-nonservative?
Conservative, since ∇x
E = 0.
LATE EDIT: sorry, this statement is not necessarily correct. The reason the field is conservative is that there is no net curl within any closed loop in the region.
BTW we assume self-generated B field << externally applied B field.
First, E
m + E
s = iR/L where R is the resistance of the segment A-B and i = current
.
Second, I think E
s = 0 throughout the ring since the ring assumes uniform resistance.
So E
m is uniform throughout the loop and the voltage between A and B is zero.
E
m = current x total loop resistance/total loop length. All E
m firelds are assumed > 0 and clockwise; all E
s fields are assumed counterclockwise and > 0. So current i is also clockwise.
However, the voltmeter does not read zero.
E
m is constant throughout the basic loop. However, we note that the loop can also be closed via the voltmeter circuit: A → voltmeter + wires → B → A instead of A → L → B → A.
So E
mL = E
mwl
w where E
mw is the emf field in the wires, E
sw is the static field in the wires, and l
w is the total length of the wires.
In the wires, E
mw = E
sw since E = 0 in the wires.
And E
swl
w = V = voltmeter reading.
Therefore, V = E
mL = iRL/L = iR, R = reistance of segment A-B. A is + with respect to B.
Now: you will say "that's what I said! It's iR!"
BUT - the voltage reading is NOT the potential difference between A and B. It is only by virtue of the fact that the voltmeter + wires offer an alternative path to your A-B segment in the magnetic closed loop and so induces an emf in the wires and also a potential in the wires and in the voltmeter resistor. The voltmeter reads ONLY E
swl
w.
This point is well described in the two K. McDonald papers I cited in my paper.
Sorry, I forgot to address V reading between B and C but the idea is the same and so is the result.