Just to wrap up the OP’S original post::
View attachment 231017
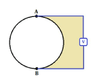
Let
d1 = length of one arc (=2πa/3),
d2 = length of one side of the triangle,
S = area A-B,
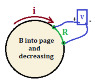
The strategy is to irradiate (apply the B field to) the triangle area A-B-C and area A-B separately, then vectorially add the various E
s and E
m (static and emf) fields by superposition. The other segments, not abutting the A-B loop, can be ignored altogether; whether or not they are irradiated does not affect the E fields in the two A-B segments.
We first note that when just the triangle area is irradiated. there is no E
s field. This means that the triangle area can also be ignored since potential differences are line-integrated E
s fields only.
So we irradiate S only:
If E
m = emf field around the A-B loop and i the corresponding current,
emf = E
m(d1 + d2) = -S dB/dt = i(r1 + r2) so we know E
m and i;
and if
E
s1 = static field along arc AB,
E
s2 = static field along the triangle side AB,
from the basic relation
j = σ
E,
j = current density,
E =
Em +
Es, we get
i = (E
m - E
s1)d1/r1 or
E
s1 = (1/d1)(E
m d1 - i r1) = E
m - i r1/d1
and similarly
E
s2 = r2 i/d2 - E
m.
Then ΔV = E
s1 d1 = E
s2 d2.
The rest is geometry and substitution.
Note that this computation is not that of a voltmeter (by all we have discussed so far) measuring voltage between A and B. The voltmeter reading is in fact VB - VA = -r1 i.