Faucet connected to water tower

[toothpaste666]

Homework Statement

A 1 cm radius pipe connects a 3 m tall water tower to a faucet.
(a) What is the gauge pressure at the faucet when the faucet is closed
(b)12 What is the gauge pressure at the faucet if the faucet is opene
d so that there is a flow of 0.2 Liter/s? Assume that the water flow is laminar.

Homework Equations

P_1 + .5d(v_1)^2 + d(y_1) = P_2 + .5d(v_2)^2 + d(y_2)
d = density , P = pressure ,y = height, v = velocity
(A_1)(v_1) = (A_2)(v_2)
A = area v = velocity

The Attempt at a Solution

for part a)
if the faucet is closed, gauge pressure at the faucet would simply be
P = dgy = (1000 kg/m^2)(9.8 m/s^2)(3 m)

for part b)

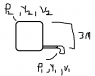
i must use bernoulli's equation. looking at the picture i drew I can say P_2 is 0, v_2 is 0 (because it is negligible), y_2 = 3 m , and y_1 = 0

to find v_1 :
use Av where v = l/t
Av = A(l/t) = Vol/t (which they give us as .2 liter/s = 2E-4 m^3/s)
A = pi r^2 = pi (.01 m) ^2 = 3.14 E-4
Av = Vol/t
(3.14E-4)v = 2E-4
v = 2/3.14 = .637 = v_1

using bernoullis:
P_1 + .5d(v_1)^2 + d(y_1) = P_2 + .5d(v_2)^2 + d(y_2)
P_1 + .5d(.637)^2 + d(0) = 0 + .5d(0)^2 + d(3)
P_1 + .5(1000)(.637)^2 = 3(1000)
P_1 = 3000 - .5(1000)(.637)^2

im not as worried about the actual numbers but is my method correct?

 

[Miles Whitmore]

You left out a factor of g in Bernoulli's Equation, but besides that your method looks good

 

[haruspex]

$P = dgy = (1000 kg/m^2)(9.8 m/s^2)(3 m)$

$(1000 kg/m^3)$

$P_1 + .5d(v_1)^2 + d(y_1) = P_2 + .5d(v_2)^2 + d(y_2)$

What dimension does $d(y_1)$ have? Something missing?

 

[toothpaste666]

oops! it should be d(y_1)g

and good catch i meant 1000 kg/m^3
sorry for the sloppiness =[