question dude said:
I'm kinda in two minds, I suspect that is wrong because wouldn't the fact that they attract each other (instead of repelling) means that the diagram would be drawn differently?
question_dude, there have been a few good answers here, but I think your above question indicates a bit of confusion that hasn't been addressed. It's important not take Feynman diagrams too literally. The only thing that matters physically is which bits are connected to what. So, when we draw the lowest order diagram for two electrons interacting, the fact that the legs for the two outgoing electrons are drawn pointing away from each isn't physically significant. So, for two electrons,
this diagram (read left to right) is the same however you choose to rotate and twist the different pieces of it. What tells us two electrons repel each other is when we actually use the diagram to calculate the probability that two electrons with particular initial momenta will scatter off each other into two electrons with two particular final momenta. If we do this, we learn that it is more likely that by exchanging a photon the electrons will be scattered away from each other than scattered towards each other—a repulsive force.
We can do the same thing with electron-positron scattering. A positron is a type of anti-matter, which means it has the same properties as an electron but opposite charge. Now, when you hear about anti-matter, you usually just here about it annihilating matter—so you might think the electron-positron interaction just destroys the two particles (and releases energy). That's one possibility, but they can also just scatter of each other by Coulomb attraction (or, rather, the quantum interaction that creates Coulomb interaction on large scales). The lowest level diagram for that process looks like
this (read left to right). Notice how similar this looks to the other diagram! In fact, this diagram isn't quite right as the arrows on the two top legs should point the other way. Those arrows are supposed to tell us whether its an electron or a positron, (
not which way its travelling. Unfortunately, this is the best I could find. In any case, the electron and the positron attract each other, even though it doesn't look like it here! To actually see that they attract, you again would need to use this diagram to calculate the scattering probabilities for different starting and ending momenta. You would see the final momenta corresponding to the two particles being attracted to each other are the most likely. We can also, by making some approximations and comparing with non-relativistic quantum mechanics, show that these two diagrams give rise to exactly the same "Coulomb's law" you learn in school for the force between like or different charges.
However, as someone else mentioned, these diagrams aren't the whole story. They're only what are called "lowest order" diagrams (and even then, not all of them). To calculate the total probability something will happen, we have add up the contribution of every possible way it can happen. These diagrams are just some of the simpler ones. For electron scattering, we also have
this diagram (read it from bottom to top—I'm sorry, there's no consistent convention for this): two electrons exchange a photon which along the way spontaneously turns into an electron and positron which very quickly annihilate back into a photon. There are an infinite number of diagrams with more and more vertices all contributing to the same process—and, in theory, we have to add them all up. This isn't possible, so instead we just approximate by adding up a few of the diagrams with small numbers of vertices. The higher order diagrams don't contribute much anyways because they have very low probabilities of happening.
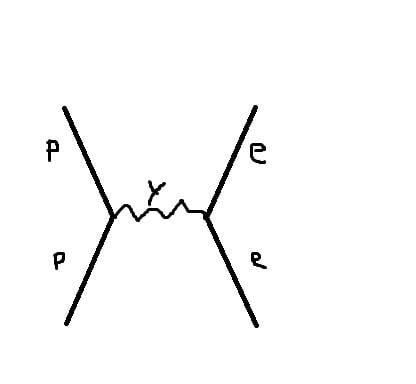
Finally, as other people have said, the diagrams for an electron scattering off a proton are not as straightforward because protons are made of quarks, and
those are what the electrons actually interact with. Electron-positron scattering is much simpler and makes the same point. However, if you add up the contributions of the various low order (two vertex) diagrams for a proton and an electron, you can represent them in a sort of short hand with something looking like the electron-electron and electron-positron diagrams (though instead of arrows on the lower two legs, which mean electron or positron depending on the direction, you would just have to write 'proton'). Just keep in mind that, unlike the two examples above, this is not an elementary process but a combination of multiple processes.