mainguy
- 15
- 0
As always a fairly devious problem from Feynman, it's getting the better of me and I imagine some of you may be able to solve!
Excuse the poor drawing. He writes 'Consider cylinders radius πcm, he cylinders are chopped into thirds and two thirds are connected as shown in fig. The thirds have uniform mass densities, but different total masses - one has 2M the other M. Find the force exerted by the wall on the cylinder'
*Note, the radial line from the center of cylinder across mass M sector is parallel to the x-axis.
So how I solved this was by finding the center of mass, which I found to be 1.256cm from the center and at 23.5 degrees to the horizontal. I then proceeded to calculate the torque of the this center of mass about the pivot point which is directly below the center.
And then by equating this torque to that exerted by the wall (which I found to be Ffriction*pi) I found F.
I got it wrong by a long way, the actual answer is 8.1N and my force was 84N...
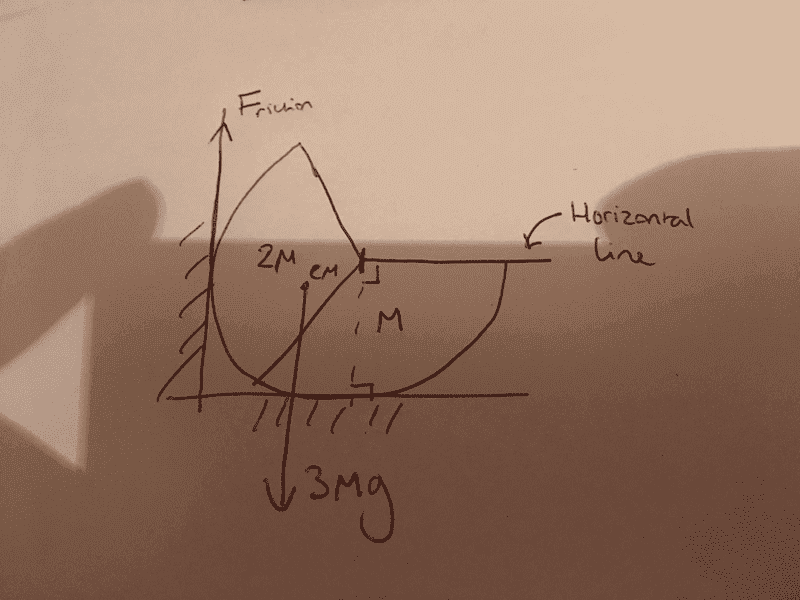
Excuse the poor drawing. He writes 'Consider cylinders radius πcm, he cylinders are chopped into thirds and two thirds are connected as shown in fig. The thirds have uniform mass densities, but different total masses - one has 2M the other M. Find the force exerted by the wall on the cylinder'
*Note, the radial line from the center of cylinder across mass M sector is parallel to the x-axis.
So how I solved this was by finding the center of mass, which I found to be 1.256cm from the center and at 23.5 degrees to the horizontal. I then proceeded to calculate the torque of the this center of mass about the pivot point which is directly below the center.
And then by equating this torque to that exerted by the wall (which I found to be Ffriction*pi) I found F.
I got it wrong by a long way, the actual answer is 8.1N and my force was 84N...