Find Angle Between Vectors C & D Using Alpha, Beta & Theta

  • Thread starter Thread starter meanyack
  • Start date Start date
  • Tags Tags
    Angle Urgent
AI Thread Summary
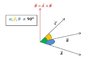
To find the angle between vectors C and D using angles α, β, and θ, the discussion emphasizes the use of the cross product and dot product formulas. The cross product formula, u X v = |u||v|sin(angle), can be rearranged to solve for the angle, but complications arise when considering the angle between vector C and the plane formed by vectors A and B. Participants express concerns about the complexity of this calculation and seek simpler methods to determine the angle. The conversation highlights the need for clarity in vector relationships and the potential challenges in applying standard formulas in this context. Overall, the thread seeks an efficient approach to calculate the angle between the specified vectors.
meanyack
Messages
19
Reaction score
0

Homework Statement



Please find the attachment for vectors. If I know \alpha, \beta & \theta (colored angles) how can I find the angle between vectors C and D in terms of \alpha, \beta & \theta?

Homework Equations



Cross product & dot product

The Attempt at a Solution

 

Attachments

  • vectors.JPG
    vectors.JPG
    13.6 KB · Views: 423
Physics news on Phys.org
The cross product is defined by u X v = |u||v|sin(angle). Solve for the angle.
 
At first glance, it seems easy. But when you try to find the angle between vector C and plane consisting A and B, then it seems complicated. So is there any way to calculate it easily?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Rope between inclines with maximum length of hanging middle portion
Replies
46
Views
2K
A moving boat with a flag on its mast
Replies
15
Views
899
Angle that makes kinetic and potential energy of simple pendulum equal
Replies
2
Views
1K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
936
The Relationship Between Masses and Angles in a Pulley System
Replies
29
Views
3K
The derivative of the dot product "distributes" over each vector
Replies
5
Views
666
The speed of the point of intersection of two uniformly moving lines
Replies
24
Views
1K
Minimum distance between balls connected by rods
Replies
9
Views
2K
Swimming to and fro across a river
Replies
5
Views
2K
Double slit: ratio of intensity of 3rd- and 0th-order maxima
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top