- 1,753
- 143
3. Suppose the charge q2 in Figure 19-30 can be moved left or right along the line connecting the charges q1 and q3, rather than sitting at a distance d from each. Given that q = 15 µC, find the distance from q1 where q2 experiences a net electrostatic force of zero. (The charges q1 and q3 remain separated by a fixed distance of 2d=38 cm.)
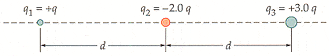
As I stare at this, it seems like there should be an easier way than the way I did it:
<br /> \begin{array}{l}<br /> k\frac{{q_{1} \,q_2 }}{{d_{1,2}^2 }} = k\frac{{q_{2} \,q_3 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \rlap{--} k\frac{{q_{1} \,q_2 }}{{d_{1,2}^2 }} = \rlap{--} k\frac{{q_{2} \,q_3 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{q \times 2q}}{{d_{1,2}^2 }} = \frac{{2q \times 3q}}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{2q^2 }}{{d_{1,2}^2 }} = \frac{{6q^2 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{2\rlap{--} q^{\rlap{--} 2} }}{{d_{1,2}^2 }} = \frac{{6\rlap{--} q^{\rlap{--} 2} }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{d_{2,3}^2 }} \\ <br /> \\ <br /> d_{2,3} = 0.38 - d_{1,2} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{\left( {0.38 - d_{1,2} } \right)^2 }} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{\left( {0.38 - d_{1,2} } \right)\left( {0.38 - d_{1,2} } \right)}} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{0.38^2 - 0.76d_{1,2} + d_{1,2}^2 }} \\ <br /> \\ <br /> 2\left( {0.38^2 - 0.76d_{1,2} + d_{1,2}^2 } \right) = 6d_{1,2}^2 \\ <br /> \end{array}<br />
<br /> \[<br /> \begin{array}{l}<br /> 0.38^2 - 0.76d_{1,2} = 2d_{1,2}^2 \\ <br /> \\ <br /> - 2d_{1,2}^2 - 0.76d_{1,2} - 0.38^2 = 0 \\ <br /> \\ <br /> d_{1,2} = \frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}} \\ <br /> \\ <br /> d_{1,2} = \frac{{ - \left( { - 0.76} \right) \pm \sqrt {\left( { - 0.76} \right)^2 - 4 \times - 2 \times - 0.38^2 } }}{{2 \times - 2}} \\ <br /> \\ <br /> d_{1,2} = - 0.51908965 \\ <br /> d_{1,2} = 0.13908965 \\ <br /> \end{array}<br />
With 0.139 m or (13.9 cm) being the correct answer
As I stare at this, it seems like there should be an easier way than the way I did it:
<br /> \begin{array}{l}<br /> k\frac{{q_{1} \,q_2 }}{{d_{1,2}^2 }} = k\frac{{q_{2} \,q_3 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \rlap{--} k\frac{{q_{1} \,q_2 }}{{d_{1,2}^2 }} = \rlap{--} k\frac{{q_{2} \,q_3 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{q \times 2q}}{{d_{1,2}^2 }} = \frac{{2q \times 3q}}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{2q^2 }}{{d_{1,2}^2 }} = \frac{{6q^2 }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{{2\rlap{--} q^{\rlap{--} 2} }}{{d_{1,2}^2 }} = \frac{{6\rlap{--} q^{\rlap{--} 2} }}{{d_{2,3}^2 }} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{d_{2,3}^2 }} \\ <br /> \\ <br /> d_{2,3} = 0.38 - d_{1,2} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{\left( {0.38 - d_{1,2} } \right)^2 }} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{\left( {0.38 - d_{1,2} } \right)\left( {0.38 - d_{1,2} } \right)}} \\ <br /> \\ <br /> \frac{2}{{d_{1,2}^2 }} = \frac{6}{{0.38^2 - 0.76d_{1,2} + d_{1,2}^2 }} \\ <br /> \\ <br /> 2\left( {0.38^2 - 0.76d_{1,2} + d_{1,2}^2 } \right) = 6d_{1,2}^2 \\ <br /> \end{array}<br />
<br /> \[<br /> \begin{array}{l}<br /> 0.38^2 - 0.76d_{1,2} = 2d_{1,2}^2 \\ <br /> \\ <br /> - 2d_{1,2}^2 - 0.76d_{1,2} - 0.38^2 = 0 \\ <br /> \\ <br /> d_{1,2} = \frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}} \\ <br /> \\ <br /> d_{1,2} = \frac{{ - \left( { - 0.76} \right) \pm \sqrt {\left( { - 0.76} \right)^2 - 4 \times - 2 \times - 0.38^2 } }}{{2 \times - 2}} \\ <br /> \\ <br /> d_{1,2} = - 0.51908965 \\ <br /> d_{1,2} = 0.13908965 \\ <br /> \end{array}<br />
With 0.139 m or (13.9 cm) being the correct answer