You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find Elevation at Point A - Math Homework
- Thread starter MrMechanic
- Start date
AI Thread Summary
The discussion focuses on calculating the elevation at point A using pressure equations in a system of two connected tanks. Participants clarify the conversion of pressure units and the significance of specific gravity, emphasizing its role in determining density relative to water. There is confusion regarding the negative pressure reading and how to correctly apply it in calculations. The importance of consistent units throughout the calculations is highlighted, particularly the distinction between mass and weight. The conversation concludes with a need to clarify the density of water in the appropriate units for accurate calculations.
Physics news on Phys.org
- 42,656
- 10,435
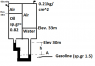
I'm not sure I understand the diagram. It appears to be two tanks side by side, connected by a pipe at the bottom and sealed at the top. Pressures in the airspaces in the tanks are given. Right?
So, now calculate the pressures at 33m in each, then at 30m in each, etc.
So, now calculate the pressures at 33m in each, then at 30m in each, etc.
MrMechanic
- 46
- 0
Yes the pressure in the airspaces in the tanks are given.
I'll start with the left tank
P = Patm + (0.82)(9.81)(38-30)
is it correct?
I'll start with the left tank
P = Patm + (0.82)(9.81)(38-30)
is it correct?
- 42,656
- 10,435
If by Patm you mean the pressure of the air in that tank, that term is ok. But watch out for the units in the other term. What does "specific gravity" mean exactly?MrMechanic said:Yes the pressure in the airspaces in the tanks are given.
I'll start with the left tank
P = Patm + (0.82)(9.81)(38-30)
is it correct?
MrMechanic
- 46
- 0
Specific gravity is the ratio of the density of a substance to the density. that's why it has no unit
yes If Patm =14.7 psi = 101.325kPa = 101.325kN/m^2
and
P = 101.325 + (0.82)(9.81(38-30)
P = 36.9714 kPa
What i don't know is how to do I form an equation where i can get the height (h)
yes If Patm =14.7 psi = 101.325kPa = 101.325kN/m^2
and
P = 101.325 + (0.82)(9.81(38-30)
P = 36.9714 kPa
What i don't know is how to do I form an equation where i can get the height (h)
- 42,656
- 10,435
OK, but you need to specify the reference substance. Did you meanMrMechanic said:Specific gravity is the ratio of the density of a substance to the density. that's why it has no unit
Specific gravity is the ratio of the density of a substance to the density of water.
?The density of that substance should therefore figure in the formula. As it stands you have (spec grav) * (acceleration) * ( height), which has dimension L2/T2.
If you continue to work out the pressure at each height, working down from the top, and put in an unknown h for the height you need, you eventually get to two expressions for the pressure right at at the bottom. They must be equal, of course.What i don't know is how to do I form an equation where i can get the height (h)
MrMechanic
- 46
- 0
is this correct?
(-40) + (0.82)(9.81)(38-30) + (1.5) (9.81) (h) - (9.81)(h+3) - 20.6 = P1
and i'll perform another on the other side? or should I set P1 = 0?
(-40) + (0.82)(9.81)(38-30) + (1.5) (9.81) (h) - (9.81)(h+3) - 20.6 = P1
and i'll perform another on the other side? or should I set P1 = 0?
MrMechanic
- 46
- 0
When I perform P1 = 0
I get h = 5.235
I get h = 5.235
- 42,656
- 10,435
Two problems.MrMechanic said:is this correct?
(-40) + (0.82)(9.81)(38-30) + (1.5) (9.81) (h) - (9.81)(h+3) - 20.6 = P1
and i'll perform another on the other side? or should I set P1 = 0?
1. I had been ignoring the minus sign in "-30cm Hg". I don't understand how an absolute air pressure can be negative. These are sealed containers, so it shouldn't be relative to ambient pressure. Do you have any explanation for that?
2. You are ignoring my comment about density and units. If the s.g. is 0.82 relative to water, what is the density in kg/m3?
MrMechanic
- 46
- 0
The minus sign is not an absolute pressure i think.
The density of oil is not given. And also gasoline. In order to get their density you have to multiply their specific gravity to the density of water which is 9.81kg/m^3
The density of oil is not given. And also gasoline. In order to get their density you have to multiply their specific gravity to the density of water which is 9.81kg/m^3
- 42,656
- 10,435
No, that's where you are going wrong. The 9.81 is gravitational acceleration. That factor converts mass to weight. The density of water is much larger.MrMechanic said:to get their density you have to multiply their specific gravity to the density of water which is 9.81kg/m^3
MrMechanic
- 46
- 0
Oh yeah sorry. It's not kg/m^3 ... It's 9.81 kN/m^3 forgot to change that sorry
- 42,656
- 10,435
Right, but answer my other question; what is the density of water in these units?MrMechanic said:Oh yeah sorry. It's not kg/m^3 ... It's 9.81 kN/m^3 forgot to change that sorry
Similar threads
- Replies
- 4
- Views
- 1K
- Replies
- 12
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 4K
- Replies
- 9
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 4K
- Replies
- 4
- Views
- 4K
- Replies
- 8
- Views
- 3K
- Replies
- 14
- Views
- 2K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math