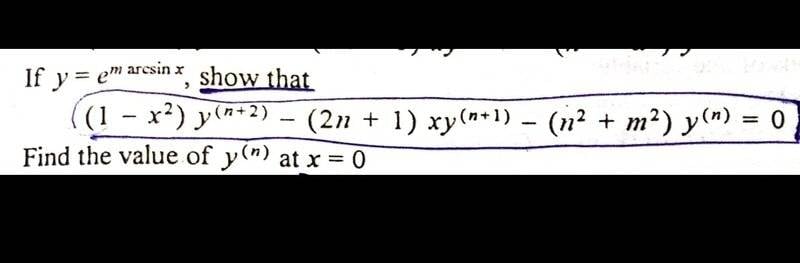Kumail Haider said:
I've no idea how to type all these mathematical expressions.

The
##\LaTeX## Guide link is at the bottom left of the edit window !
But I grant you it's an awful lot of work... pure masochism to typeset all that stuff

So you start with
$$y^{(0)} = y = e^{m\arcsin x} \ \Rightarrow \ y^{(1)} = {m\over \sqrt{1-x^2}} \; e^{m\arcsin x} = {m\over \sqrt{1-x^2}} \; y$$and so $$
\begin {align*} y^{(2)} &= \left ( {m\over \sqrt{1-x^2}} \right )' \;y +{m\over \sqrt{1-x^2}} \; y' \\ \ \\
&={x\over 1-x^2} \left ( {m\over \sqrt{1-x^2}} \right ) \;y + {m^2\over 1-x^2} \;y \\ \ \\
&= {x\over 1-x^2}\; y^{(1)} + {m^2\over 1-x^2} \;y ^{(0)} \qquad\Rightarrow \\ \ \\
\left (1-x^2 \right )\; y^{(2)} &= x \; y^{(1)} + m^2\;y^{(0)} \tag 1
\end {align*}
$$Leibnitz proof is by induction, so with ##(1)## we have a statement ##P_{n=0}## :
$$\begin {align*} \left (1-x^2 \right )\; y^{(n+2)} &= (2n+1)\;x \; y^{(n+1)} + (n^2+m^2)\;y^{(n)} \tag 2\end {align*} $$ which is true for all ##n## if we can prove ##P_{n}\Rightarrow P_{n+1}##.
To do that we differentiate ##(2)##:
$$\begin {align*} -2x \; y^{(n+2)} + \left (1-x^2 \right ) \; y^{(n+3)} &= (2n+1) \; y^{(n+1)} + (2n+1)\;x \; y^{(n+2)} + (n^2+m^2)\;y^{(n+1)} \\ \ \\
\left (1-x^2 \right ) \; y^{(n+3)} &= (2n+3)\;x \; y^{(n+2)} + (n^2+ 2n+1+m^2)\;y^{(n+1)} \\ \ \\
\left (1-x^2 \right ) \; y^{(n+3)} &=\left (2(n+1)+1\right )\;x \; y^{(n+2)} + \left ( (n+1)^2+ m^2\right )\;y^{(n+1)}
\end {align*} $$which is ##P_{n+1}##.
So there ! But you had already done that, witness the pictures :
Kumail Haider said:
I've done the first part that is prove
Now on to the ninth derivative, one way or the other.
Cheating isn't allowed, I suppose (anyway, the
ninth derivative looks horrendous and I don't know if I can trust the result when my cheater
substitutes ##x=0## 
)
And therefore, all I can come up with is brute force: use ##(2)## four times to ripple down from ##y^{(9)}## to ##y^{(1)}## which is ##m##.
That is from ##n=7## in three steps of 2 to to ##n=1##.
Fortunately, all ##y^{(n+1)}## have a factor ##x## in front, so they drop out at ##x=0##.
That means: at ##x=0## we have ##y^{(9)} |_{x=0} ## ##= (7^2+m^2) \;y^{(7)} |_{x=0}## and so on.
So brute force yields $$y^{(9)} |_{x=0} = (49+m^2)(25+m^2)(9+m^2)(1+m^2)m$$And I am way too lazy to work this out myself. But it turns out the
cheater is pretty consistent with ##m(m^8 + 84 m^6 + 1974 m^4 + 12916 m^2 + 11025)## as before. Hurray!
And as a farewell present, usable for the umpteenth derivative as well:$$y^{(2n+1)} |_{x=0} = m\;\prod_{k=1}^n \left( (2k-1)^2+m^2\right ) $$I think ...
[edit] And it's pure fun to do ##y^{(2n)} |_{x=0} ## and find (almost) the same expression ! Am I overdoing...?
(but now I have robbed you of your exercise... violating PF rules. Sorry about that, but I couldn't resist

)
Let me pick up at your
##A## is correct, but ##B## seems to be in error. I leave it to you to find the minus sign in your picture ....

##\ ##