- #1
jamesbrewer
- 13
- 0
Homework Statement
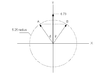
Two vectors A and B have the same magnitude of 5.25. If the sum of these two vectors gives a third vector equal to 6.73j, determine the angle between A and B.
Homework Equations
For some vector [itex]\vec{R}[/itex]: [itex]|\vec{R}| = \sqrt{R_x^2 + R_y^2}[/itex]
The Attempt at a Solution
I feel like I need to find the components of A and B, but I can't figure out how to do that with only the information given -- is it even possible?
I think the magnitude of the third vector is 6.73. Since there was no [itex]\hat{i}[/itex] term given for [itex]\vec{R}[/itex], I would say that [itex]|\vec{R}| = \sqrt{R_x^2 + R_Y^2} = \sqrt{6.73^2} = 6.73[/itex].
Given the components of A and B, this would be easy to solve. Without them I am utterly lost. What am I missing?