beefiestcrib55
- 1
- 0
1. Homework Statement
The curve of y= 4/(x^2+4), the x-axis, and the vertical lines x = -2 and x = 2
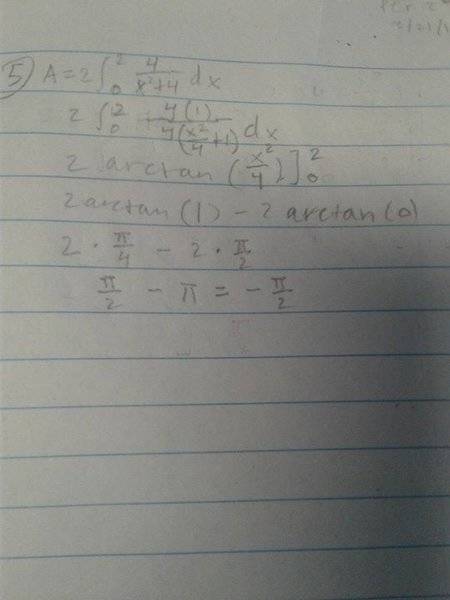
The curve of y= 4/(x^2+4), the x-axis, and the vertical lines x = -2 and x = 2
