Find the current in the 2Ω resistor marked A

  • Thread starter Thread starter fishy
  • Start date Start date
  • Tags Tags
    Current Resistor
AI Thread Summary
To find the current in the 2Ω resistor marked A, it's essential to apply Ohm's Law (V=IR) along with the Loop and Junction Rules. The circuit consists of three sections, including an 8Ω-2Ω path on the left and an 8Ω-2Ω-3Ω path on the right, with the 8Ω resistor appearing to be shorted. Understanding how these sections interact is crucial for determining the current through resistor A. The left and right sections influence the overall current distribution, which needs to be analyzed to solve the problem effectively. Clarifying these relationships will aid in completing the solution.
fishy
Messages
2
Reaction score
0

Homework Statement



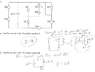
I attached the image, but it's asking me to find the current in the 2Ω resistor marked A.


Homework Equations



V=IR
Loop Rule
Junction Rule: I(in)=I(out(

The Attempt at a Solution



I have no solution. I just conceptually don't understand how my professor worked this problem and would like any guidance on what he did or some other way to complete this problem.
 

Attachments

  • PWORx93.png
    PWORx93.png
    19.4 KB · Views: 606
Physics news on Phys.org
There are basically 3 sections to the circuit, the 8ohm-2ohm path on the left, the 8 ohm (which appears to be shorted)-2ohm-3ohm path on the right and the all the stuff in the middle.

What effect do the left and right sections have on the current through resistor A ?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Why is current constant through a resistor?
Replies
11
Views
1K
Finding Current in Resistors & Charge of Capacitor
Replies
4
Views
2K
Solve Kirchhoff's Laws Homework: Find Current I in a Circuit
Replies
2
Views
1K
Kirchhoff's law: Find the current I3 through the Amp meter
Replies
4
Views
2K
Finding the Current in a Resistor in a Closed Circuit
Replies
4
Views
2K
Solving Resistor Circuits: Find Currents in R & 10Ω Resistors
Replies
3
Views
1K
Navigate the Res-Monster Maze: Find R's Current
Replies
6
Views
4K
Finding the Current Through a Resistor (Working With Parallel and Series)
Replies
3
Views
1K
Two concentric conducting spherical shells and resistor in between
Replies
44
Views
4K
Find the equivalent resistance of this circuit
Replies
31
Views
4K

Hot Threads

Recent Insights

Back
Top