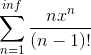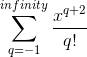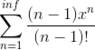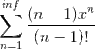Find the expression for the sum of this power series

[Kqwert]

Homework Statement

Hello,

I need to find an expression for the sum of the given power series

The Attempt at a Solution

I think that one has to use a known Maclaurin series, for example the series of e^x. I know that I can rewrite

, which makes the expression even more similar to the Maclaurin series for e^x. Any help?

 

[Orodruin]

I think that one has to use a known Maclaurin series, for example the series of e^x.

This is a good idea. You may want to use the fact that $n = (n-1) + 1$ rather than going for getting $n!$ in the denominator though.

 

[Kqwert]

This is a good idea. You may want to use the fact that $n = (n-1) + 1$ rather than going for getting $n!$ in the denominator though.

How does that help me?

 

[Orodruin]

How does that help me?

Did you try doing it?

 

[Kqwert]

Did you try doing it?

Yes, but not sure what it helps me? Should I replace all n's in the expression by n = (n-1)+1?

 

[Orodruin]

No, just in the numerator to split your sum into two.

It also helps if you state what you get when you do so - otherwise I have to guess what stage you are at.

 

[Kqwert]

So I get this expression?

 

[Orodruin]

I assume you mean $x^n$. So split it into two sums and treat each sum separately. You may want to simplify the second term change the summation variable in both sums.

 

[Kqwert]

I assume you mean $x^n$. So split it into two sums and treat each sum separately. You may want to simplify the second term change the summation variable in both sums.

Yeah, I mean x^n! What do you mean by change the summation variable. Is it like write k = n-1?

 

[Orodruin]

Is it like write k = n-1?

Yes, that could be a reasonable substitution for one of the terms.

 

[Kqwert]

Yes, that could be a reasonable substitution for one of the terms.

What about the last term though? Not sure what the best simplification of that is.

 

[Orodruin]

What about the last term though? Not sure what the best simplification of that is.

What is $(n-1)/(n-1)!$?

 

[Kqwert]

What is $(n-1)/(n-1)!$?

You can split that expression into two as well..?

 

[Orodruin]

What is $(n-1)!$?

 

[Kqwert]

(n-1)(n-2)(n-3)(n-4) etc.. I guess you can write 1/(n-2)!, but doubt that is it?

 

[Orodruin]

(n-1)(n-2)(n-3)(n-4) etc.. I guess you can write 1/(n-2)!, but doubt that is it?

Why do you doubt that?

 

[Kqwert]

Why do you doubt that?

Hm, I guess I can substitute k = n-2, which makes it into the exponential Maclaurin Series?

 

[Orodruin]

Hm, I guess I can substitute k = n-2, which makes it into the exponential Maclaurin Series?

Does it? What exactly do you obtain?

 

[Kqwert]

So i am getting a little lost here.

This is where we are right?
By substituting k = n-1 into the first expression we get a very similar expression to the e^x series,

in the second expression we can do q = n - 2 and get..

is this the way?

 

[Orodruin]

You are making good progress. So what is the difference between the two series that you have obtained and the expansion of $e^x$?

 

[Kqwert]

Just x and x^2, respectively, which are not dependent on n. However, what happens when I do the variable changes and calculate the sums? For k = n-1 we get k = 0 as the lower sum and k = inf. as the upper sum, while we get q = -1 as the lower and q = inf as the upper for the second expression?

 

[Orodruin]

Just x and x^2, respectively, which are not dependent on n. However, what happens when I do the variable changes and calculate the sums? For k = n-1 we get k = 0 as the lower sum and k = inf. as the upper sum, while we get q = -1 as the lower and q = inf as the upper for the second expression?

Yes, this is indeed the next thing you must check. For the k sum, you are already fine since the exponential series expansion is a sum from zero. For the q sum, what is $(n-1)/(n-1)!$ when $n = 1$? Does that term contribute?

 

[Kqwert]

Yes, this is indeed the next thing you must check. For the k sum, you are already fine since the exponential series expansion is a sum from zero. For the q sum, what is $(n-1)/(n-1)!$ when $n = 1$? Does that term contribute?

It´s just zero. But, the way I have done it. I´m left with

WolframAlpha gave me x^2*e^x, but why..? I know that we must get q = 0, which results in x^2*e^x, but doesn't the q = -1 term contribute?

 

[Orodruin]

You have to treat that term separately. Before cancelling (n-1)/(n-1)! to 1/(n-2)!, note that the n = 1 term reads 0/0!

 

[Kqwert]

You have to treat that term separately. Before cancelling (n-1)/(n-1)! to 1/(n-2)!, note that the n = 1 term reads 0/0!

But why does that matter when the expression has been re-written? isn't is possible to solve it from the re-written series?

 

[Orodruin]

Because the rewriting is not correct for $n = 1$.

 

[Kqwert]

Because the rewriting is not correct for $n = 1$.

Not sure If I understand what you mean?

 

[Orodruin]

For $n = 1$, the term reads $0/0!$ but with the "cancellation" you did, it would be $-1/(-1)!$, which you would need to interpret in terms of the Gamma function $\Gamma(x)$ in the limit $x \to 0$, where $\Gamma(x) \to \infty$. It is much easier to just remove that term from the beginning since 0! = 1 and therefore 0/0! = 0/1 = 0.

 

[Kqwert]

For $n = 1$, the term reads $0/0!$ but with the "cancellation" you did, it would be $-1/(-1)!$, which you would need to interpret in terms of the Gamma function $\Gamma(x)$ in the limit $x \to 0$, where $\Gamma(x) \to \infty$. It is much easier to just remove that term from the beginning since 0! = 1 and therefore 0/0! = 0/1 = 0.

Ok thanks, but how does that relate to the "q-series" I´ve found which starts at q = -1? Wrong way of doing it?

 

[Orodruin]

Ok thanks, but how does that relate to the "q-series" I´ve found which starts at q = -1? Wrong way of doing it?

You only found that particular series by making the cancellation. Alternatively you can do the replacement before cancellation, you will then get $(q+1)/(q+1)!$ and you can note that the $q = -1$ term is zero because $q+1 = 0$ so you can remove it. After that the cancellation is fine for all terms.

 

[Kqwert]

Thank you, but what cancellation? Re-writing (n-1)/(n-1)! to 1/(n-2)! ? Not sure if I understand exactly what happens and why.

 

[Orodruin]

Thank you, but what cancellation? Re-writing (n-1)/(n-1)! to 1/(n-2)! ? Not sure if I understand exactly what happens and why.

Yes, that cancellation. Because, as I said in #24, for $n = 1$, that term reads $0/0!$ and the terms you would cancel are 0 and 0, which you cannot do. You have to look at that term separately and realize that it is actually zero so that it gives no contribution.

 

[Kqwert]

Yes, that cancellation. Because, as I said in #24, for $n = 1$, that term reads $0/0!$ and the terms you would cancel are 0 and 0, which you cannot do. You have to look at that term separately and realize that it is actually zero so that it gives no contribution.

I understand that, but I don't understand the order of things. When we start from

Should we first say that

and then do the change of variables? I am becoming a bit confused re. the best way of solving this.

 

[Orodruin]

What you had from the beginning was
$$
\sum_{n=1}^\infty \frac{(n-1)x^n}{(n-1)!},
$$
not the sum from $n = 0$. It does not matter if you change variables first or if you do the cancellation first. The only thing you must do is to remove the term $n = 1$ (or equivalently $q = -1$) before you do the cancellation because that step is not valid for that term.

 

[Kqwert]

And by removing the n = 1 term we end up starting at n = 2, right?

 

[Orodruin]

Yes, which means $q = 0$.

 

[Kqwert]

Excellent, thanks a lot for the help!

 

[Orodruin]

So now that you have worked through it, let me just mention an alternative approach, which is how I initially did it but it involves some extra trickery using derivatives. The aim is to reduce the remaining series to that of the exponential function by extracting powers of $x$ and using a derivative relation.

The point is to note that $n x^{n-1}$ is the derivative of $x^n$. We have
$$
\sum_{n=1}^\infty \frac{nx^n}{(n-1)!} = x \sum_{n=1}^\infty \frac{n x^{n-1}}{(n-1)!} = x \frac{d}{dx} \sum_{n=1}^\infty \frac{x^{n}}{(n-1)!}
$$
where in the first step we have just factorised out an $x$ and in the second we applied the derivative relation. Now we can extract another factor $x$ from the sum and end up with
$$
\sum_{n=1}^\infty \frac{nx^n}{(n-1)!} = x\frac{d}{dx}\left(x \sum_{n=1}^\infty \frac{x^{n-1}}{(n-1)!}\right)
= x\frac{d}{dx}\left(x \sum_{m=0}^\infty \frac{x^{m}}{m!}\right) = x \frac{d}{dx}(x e^x) = x (x e^x + e^x) = x(1+x) e^x,
$$
where in the middle we did the substitution $m = n-1$ then used the power series for $e^x$ and regular differentiation. Luckily, this is the same result as you got.

 

[Ray Vickson]

Excellent, thanks a lot for the help!

I notice that you were getting all mixed up with summations (what terms should be removed, how should the sums be re-indexed, etc?). When I solve such problems I try to avoid all that by writing out a few terms explicitly:
$$S = \sum_{n=1}^\infty \frac{n x^n}{(n-1)!} = x + \frac{2 x^2}{1!}+\frac{3 x^3}{2!} + \frac{4 x^4}{3!} + \cdots + \frac{n x^n}{(n-1)!} + \cdots $$ This can be written as
$$S = x + \frac{(1+1) x^2}{1!} + \frac{(2+1) x^3}{2!} + \frac{(3+1)x^4}{3!} + \cdots + \frac{((n-1)+1) x^n}{(n-1)!)} + \cdots, $$ so $S = S_1 + S_2,$ where
$$S_1 = x^2 + \frac{2 x^3}{2!} + \frac{3 x^4}{3!} +\cdots + \frac{(n-1) x^{n-1}}{(n-1)!} +\cdots\\ = x^2 \left(1 + x + \frac{x^2}{2!} + \cdots + \frac{x^{(n-2)}}{(n-2)!} + \cdots \right), $$ and
$$S_2 = x + x^2 + \frac{x^3}{2!} + \frac{x^4}{3!} + \cdots + \frac{x^n}{(n-1)!} + \cdots \\= x \left (1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots+ \frac{x^{n-1}}{(n-1)!} + \cdots \right).$$ The rest is easy now.

When I say that I, personally, write out a few terms (as above) I really mean it; I have found over the years that doing that eliminates a lot of confusion and is a good way of avoiding a headache.