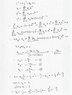s3a
- 814
- 8
Homework Statement
Problem:
Find the first eight coefficients (i.e. a_0, a_1, a_2, ..., a_7) of the power series expansion
y = ##Σ_{n = 0}^{∞}## [##a_n## ##x^n##]
of the solution to the differential equation
y'' + xy' + y = 0
subject to the initial-value conditions y(0) = 0, y'(0) = 1.
Solution:
The solution is attached as TheSolution.jpg.
Homework Equations
Power series manipulation.
Recurrence relation.
The Attempt at a Solution
I understand everything the solution says except how ##a_0## and ##a_1## were obtained. That is, I don't think understand what the author of the solutions is doing in the following step.:
y(0) = ##a_0## = 1
y'(0) = ##a_1## = 1
It seems like the initial-conditions are being used, but did the author make a mistake? I ask, because it seems to me that ##a_0## should equal 0 instead of 1.
Assuming the author of the solutions is correct, could someone please tell me what the logic is in getting those values? Looking at similar problems in my textbook, I notice what seems to be like constants that are not part of the sums in front of what seems to be two linearly independent solutions, and I don't understand what is going on.
Any help would be GREATLY appreciated!
P.S.
If more detail is needed, just ask!
P.P.S
Also, is it just me, or is the author answering a slightly different question than what the question poses?