Find the Largest Area of Triangle

[anemone]

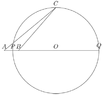
Triangle ABC has $$AB=9$$ and $$BC:AC=40:41$$. What's the largest area that this triangle can have?

 

[MarkFL]

My solution:

Spoiler

Let:

$$\overline{BC}=a$$

$$\overline{AC}=b$$

and we are told:

$$b=\frac{41}{40}a$$

Using Heron's formula, the area of the triangle as a function of $a$ is:

$$A(a)=\frac{9\sqrt{-81a^4+10499200a^2-207360000}}{6400}$$

The area is maximized where the radicand is maximized, hence:

$$\frac{d}{da}\left(-81a^4+10499200a^2-207360000 \right)=4a\left(5249600-81a^2 \right)=0$$

Discarding $a=0$, and taking the positive root, we find the critical value is:

$$a=\frac{40\sqrt{3281}}{9}$$

We know this is a maximum since the radicand is a quartic with a negative leading coefficient.

Thus, the maximum area is:

$$A_{\max}=A\left(\frac{40\sqrt{3281}}{9} \right)=820$$

 

[Opalg]

Here is a geometric way to get the same answer.
[sp]

View attachment 1081​

If the ratio $BC:AC$ is $40:41$ then $C$ must lie on an Apollonius circle with diameter $PQ$, where $P,Q$ lie on the line $AB$, with the ratios $BP:AP$ and $BQ:AQ$ both equal to $40:41$. Since $AB=9$, we must have $AP = 41/9$, $PB = 40/9$ and $BQ = 360.$ Thus the radius of the circle is $\frac12\bigl(360 + \frac{40}9\bigr) = 1640/9.$ The area of the triangle is obviously greatest when $C$ is at its maximum height above the line $AB$, in other words when it is directly above the centre of the circle. The height $OC$ is then the radius of the circle, and the area of the triangle is $\frac12AB*OC = \dfrac92\dfrac{1640}9 = 820.$​

[/sp]

 

[anemone]

Hi MarkFL and Opalg,

Thank you so much for participating in this problem.

Opalg, your solution is definitely an ingenious approach and I have talked to MarkFL and we don't think we would have thought of that geometric approach to solve this problem!

 

[MarkFL]

Hi MarkFL and Opalg,

Thank you so much for participating in this problem.

Opalg, your solution is definitely an ingenious approach and I have talked to MarkFL and we don't think we would have thought of that geometric approach to solve this problem!

Not so quick...where is your solution? (Clapping)

 

[anemone]

My solution:

We first let the three sides of the triangle ABC be $$9,\;40k,\;41k$$.

By using the Heron's formula to find the area of the triangle ABC$$(A_{\text{triangle ABC}})$$, we see that we have

$$A_{\text{triangle ABC}}=\sqrt{\left( \frac{81k+9}{2}\right)\left(\frac{81k+9}{2}-9\right)\left(\frac{81k+9}{2}-40k\right)\left(\frac{81k+9}{2}-41k\right)}$$

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac{3}{4} \sqrt{-81\left(k^4-\frac{(81^2+1)k^2}{81}+1\right)}$$

And if we let $$k^2=x$$, the equation above becomes

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac{3}{4} \sqrt{-81\left(x^2-\frac{(81^2+1)x}{81}+1\right)}$$

By completing the square of the radicand, we obtain

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac{3}{4} \sqrt{-81\left(x-\frac{3281}{81}\right)^2+\frac{3281^2}{81}-81}$$

Hence,

$$A_{\text{maximum}}=\frac{3}{4} \sqrt{\frac{3281^2}{81}-81}=820$$

Alternatively, we could approach this problem by applying AM-GM inequality if we write the radicand a bit differently.

$$A_{\text{triangle ABC}}=\sqrt{\left( \frac{81k+9}{2}\right)\left(\frac{81k+9}{2}-9\right)\left(\frac{81k+9}{2}-40k\right)\left(\frac{81k+9}{2}-41k\right)}$$

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac{1}{4} \sqrt{ 9(9k+1)(9k-1)(9+k)(9-k)}$$

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac{1}{4} \sqrt{ (9k+1)(9k-1)(81+9k)(81-9k)}$$

$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac{1}{4} \sqrt{ (81k^2-1)(81^2-81k^2)}$$

By applying AM-GM inequality to these two terms $$81k^2-1$$ and $$81^2-81k^2$$ gives

$$\frac{81k^2-1+81^2-81k^2}{2}\ge \sqrt{(81k^2-1)(81^2-81k^2)}$$

$$\sqrt{(81k^2-1)(81^2-81k^2)} \le \frac{81^2-1}{2}$$

Now, we can conclude that

$$A_{\text{maximum}}=\frac{1}{4}\left( \frac{81^2-1}{2}\right)=820$$