Taniaz
- 364
- 1
Homework Statement
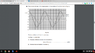
The two oscillators each have the same mass. Use Fig. 4.1 to determine (i) the phase difference between the two oscillators (picture attached)
Homework Equations
Subtracting to find the horizontal shift
The Attempt at a Solution
I found the two points where both graphs intersect the time axis and took their difference but I am getting a difference of 0.2 (pi) and the mark scheme says 1/3 (pi)?