You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find the power series in x-x0?
- Thread starter Math10
- Start date
-
- Tags
- Power Power series Series
Physics news on Phys.org
Math10
- 301
- 0
What I did was the substitution method using z=x-x0.
The answer for this problem is
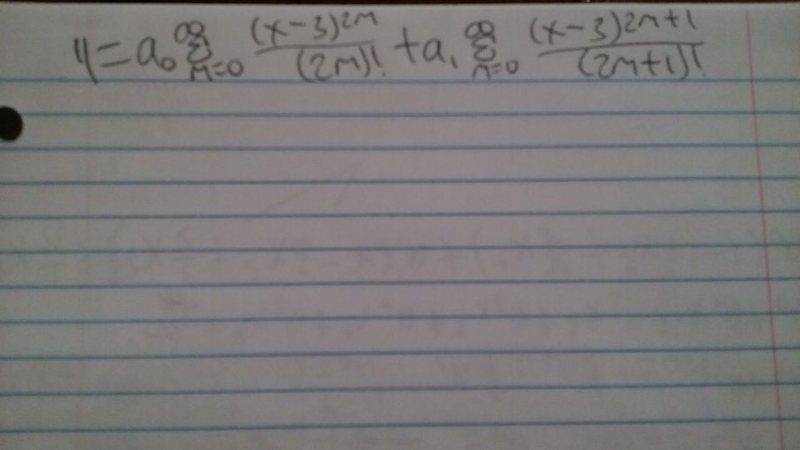
The answer for this problem is
Ray Vickson
Science Advisor
Homework Helper
Dearly Missed
- 10,704
- 1,723
Math10 said:Homework Statement
Find the power series in x-x0 for the general solution of y"-y=0; x0=3.
Homework Equations
None.
The Attempt at a Solution
Let me post my whole work:
No, please don't. The PF standard is for you to type out the problem and the solution, reserving images for things like diagrams or geometric constructions, etc.
I know that some helpers answer questions about handwritten solution images, but most will not bother. You should consult the pinned post "guidelines for Students and Helpers", by Vela, for a good explanation about this and similar issues.
Math10
- 301
- 0
Can you please take a look at the work that I posted? It's clearly written.
- 29,093
- 20,717
Math10 said:Can you please take a look at the work that I posted? It's clearly written.
It looks like the right answer in post #2, if that's all you are asking.
Math10
- 301
- 0
I know that's the right answer, but what should I do to get to the right answer after the last step in my work? That's where I got stucked.
- 29,093
- 20,717
Math10 said:I know that's the right answer, but what should I do to get to the right answer after the last step in my work? That's where I got stucked.
You need to spot a pattern in the coefficients (and verify it by induction if need be). You can see from the answer that you need to separate ##n## even and odd.
Math10
- 301
- 0
You mean this:
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
- 29,093
- 20,717
Math10 said:You mean this:
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
Yes, but can you see the pattern? The answer gives you a big clue!
Math10
- 301
- 0
So how do I get to the answer? I know where x-3 comes from.
- 29,093
- 20,717
Math10 said:So how do I get to the answer? I know where x-3 comes from.
You get to the answer by noticing that ##1 \times 2 \times 3 \times \dots \times n = n!##
The clue was that the answer has ##n!## in it.
Math10
- 301
- 0
I still don't really get it.
- 29,093
- 20,717
Math10 said:I still don't really get it.
You have:
##(n+2)(n+1)a_{n+2} = a_n##
Hence:
##a_{n+2} = \frac{a_n}{(n+2)(n+1)}##
For ##n## even this gives:
##a_2 = \frac{a_0}{2}, \ a_4 = \frac{a_2}{12} = \frac{a_0}{24}, \ a_6 = \frac{a_4}{30} = \frac{a_0}{720} \dots##
And, now by insight, inspiration (or looking at the answer) you have to notice that ##2, 24, 720 \dots## are the even factorials and hence ##a_n = \frac{a_0}{n!}##
Odd ##n## is much the same.
Math10
- 301
- 0
I got it now. Thank you so much.
berkeman
Admin
- 69,099
- 23,989
This thread is in the Homework Help forums...PeroK said:You have:
##(n+2)(n+1)a_{n+2} = a_n##
Hence:
##a_{n+2} = \frac{a_n}{(n+2)(n+1)}##
For ##n## even this gives:
##a_2 = \frac{a_0}{2}, \ a_4 = \frac{a_2}{12} = \frac{a_0}{24}, \ a_6 = \frac{a_4}{30} = \frac{a_0}{720} \dots##
And, now by insight, inspiration (or looking at the answer) you have to notice that ##2, 24, 720 \dots## are the even factorials and hence ##a_n = \frac{a_0}{n!}##
Odd ##n## is much the same.
Similar threads
- Replies
- 68
- Views
- 4K
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 8
- Views
- 2K
- Replies
- 22
- Views
- 4K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math
