mitaka90
- 9
- 0
I have no idea how to solve this problem.
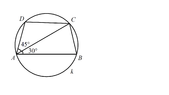
ABCD is just an irregular Quadrilateral so nothing too special with that figure.
We are looking for the ratio BC:CD and we only have that two angles. I know that the answer is 1:√2, but I have no idea how to find it.
ABCD is just an irregular Quadrilateral so nothing too special with that figure.
We are looking for the ratio BC:CD and we only have that two angles. I know that the answer is 1:√2, but I have no idea how to find it.