- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- see attached
- Relevant Equations
- Ring Theory
Going through this, am still checking but will post all the same; which method did they apply to find the roots of the attachment below.
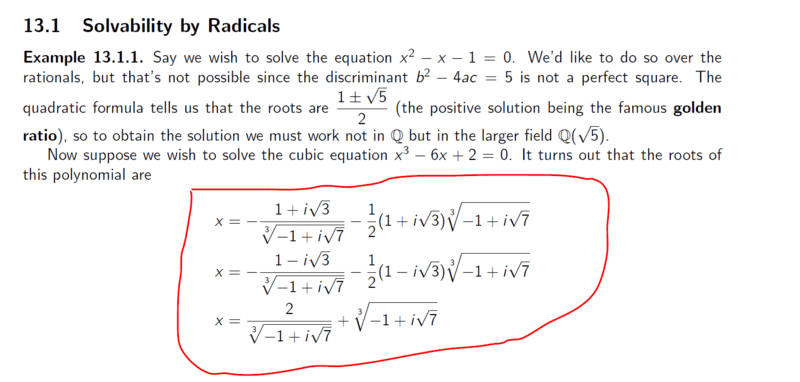 My thinking;
My thinking;
Let
##p+qi##
be the cube root of
##x^3-6x+2=0##
then,
##\sqrt{x(x^2-6)}=i\sqrt{2}##
##(p^2-q^2+2pqi)(p+qi)= x^3-6x+2##
We know that,
##\sqrt{x^3-6x}=0+ i\sqrt{2}##
...
##(p^3-pq^2)=0 ##
##\sqrt{(-3p^2q-2pq^2+q^3)}i =i\sqrt{2}##
Let
##p+qi##
be the cube root of
##x^3-6x+2=0##
then,
##\sqrt{x(x^2-6)}=i\sqrt{2}##
##(p^2-q^2+2pqi)(p+qi)= x^3-6x+2##
We know that,
##\sqrt{x^3-6x}=0+ i\sqrt{2}##
...
##(p^3-pq^2)=0 ##
##\sqrt{(-3p^2q-2pq^2+q^3)}i =i\sqrt{2}##
Last edited: