Find the tensions of two strings in mechanical equilibrium

[Davidllerenav]

Homework Statement

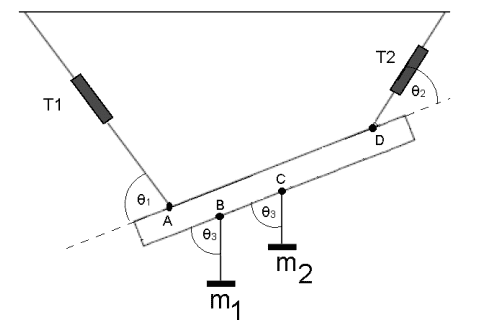
A rule of weight $w$ is supported by two strings and inclined with respect to the horizontal as shown the figure. From the points $B$ and $C$ of the rule hang two masses $m_1$ and $m_2$. Considering that the system is in mechanical equilibrium, calculate the tensions in the strings $T_1$ and $T_2$. Consider that point $C$ it's in the middle of the rule (Important: To simplify the system solution, consider only the condition $Pτ = 0$ at points $A$ and $D$.)

Relevant Equations

$\sum \vec F=0$
$\sum \tau = 0$

I tried to do the free body diagram of the problem, but I{m confused because the rule is inclined. Should I just use the given angles to calculate the forces on x and y? Also, how should I calculate the torques? Since I don't know the dimensions of the rule. Can you help me? I think that once I understand how to set up the diagrams I would be able to understand. Thr figure of the problem is shown below.

 

[Chestermiller]

Is B half-way between A and C?

 

[Davidllerenav]

Is B half-way between A and C?

It isn't in the problem statement, so I guess that we don't know where B is.

 

[haruspex]

It isn't in the problem statement, so I guess that we don't know where B is.

Quite so.

Should I just use the given angles to calculate the forces on x and y?

Yes, but how are you defining the x and y directions? Taking the line of the rule as x might be the convenient option.

I don't know the dimensions of the rule.

If all those three angles and three weights are given, I see no need to take moments. Just taking force balance in two directions gives you two equations and the two tensions are the only unknowns.

But I have a feeling that the problem is overspecified. Because there are two joints on the rule, I suspect that taking moments about two axes can yield a fourth independent equation. That would allow you to find AB and one of the angles.
I could be wrong about that - I have not tried it.

 

[Davidllerenav]

Quite so.

Yes, but how are you defining the x and y directions? Taking the line of the rule as x might be the convenient option.

If all those three angles and three weights are given, I see no need to take moments. Just taking force balance in two directions gives you two equations and the two tensions are the only unknowns.

But I have a feeling that the problem is overspecified. Because there are two joints on the rule, I suspect that taking moments about two axes can yield a fourth independent equation. That would allow you to find AB and one of the angles.
I could be wrong about that - I have not tried it.

Yes, I was using the line of the rule as x. Sí I would have $T_2\cos\theta_2-T_1\cos\theta_1-m_1g\cos\theta_3-m_2g\cos\theta_3=0$ for the x direction and $T_1\sin\theta_1+T_2\sin\theta_2-m_1g\sin\theta_3-m_2g\sin\theta_3=0$?

 

[kuruman]

Yes, I was using the line of the rule as x. Sí I would have $T_2\cos\theta_2-T_1\cos\theta_1-m_1g\cos\theta_3-m_2g\cos\theta_3=0$ for the x direction and $T_1\sin\theta_1+T_2\sin\theta_2-m_1g\sin\theta_3-m_2g\sin\theta_3=0$?

These equations are OK except that you did not include the weight $w$ of the rule. I would define a new parameter $W=m_1g+m_2g+w$ to make the algebra more compact.

 

[Davidllerenav]

These equations are OK except that you did not include the weight $w$ of the rule. I would define a new parameter $W=m_1g+m_2g+w$ to make the algebra more compact.

Ok. Then all I should do is solve for the tension?

 

[kuruman]

Yes, but there are two tensions.

 

[hurreechunder]

So you have two unknowns and two equations along the rule and perpendicular to the rule for the forces.
The torque balance will be a redundancy

 

[Chestermiller]

So you have two unknowns and two equations along the rule and perpendicular to the rule for the forces.
The torque balance will be a redundancy

No. You don’t know where point B is located. The torque balance can resolve this once the string tensions are known from the force balances.

 

[Davidllerenav]

Yes, but there are two tensions.

But I can solve one of the equations for one of them and replace that on the other, right?

 

[hurreechunder]

No. You don’t know where point B is located. The torque balance can resolve this once the string tensions are known from the force balances.

Perhaps it would help for the OP to specify what is a 'given' in the problem. If theta1, theta2, and theta3 are givens, there is no need to use torque balance as you have two equations and two unknowns. If one or all of them is not a given, then there is a need to know the location of B. In that case, if the location of Point B changes, the angles will change, as the ruler will 'swing' to balance the moments.

 

[kuruman]

Perhaps it would help for the OP to specify what is a 'given' in the problem. If theta1, theta2, and theta3 are givens, there is no need to use torque balance as you have two equations and two unknowns. If one or all of them is not a given, then there is a need to know the location of B. In that case, if the location of Point B changes, the angles will change, as the ruler will 'swing' to balance the moments.

Amen.

 

[kuruman]

But I can solve one of the equations for one of them and replace that on the other, right?

Right, but you don't even have to do that. Just put anything with $T_2$ on the left side of each of the two equations and divide one equation by the other which will eliminate $T_2$. This will give an equation in $T_1$ to solve. Repeat with anything with $T_1$ on the left side. Simplify using the trig identity $\sin(a\pm b)= \sin a \cos b\pm \cos a \sin b.$

 

[Davidllerenav]

Perhaps it would help for the OP to specify what is a 'given' in the problem. If theta1, theta2, and theta3 are givens, there is no need to use torque balance as you have two equations and two unknowns. If one or all of them is not a given, then there is a need to know the location of B. In that case, if the location of Point B changes, the angles will change, as the ruler will 'swing' to balance the moments.

All the angles are supposed to be known.

 

[kuruman]

All the angles are supposed to be known.

Then you're almost done. See post #14.