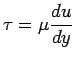Perodamh
- 20
- 0
Homework Statement
A plate having an area of 0.6m^2 is sliding down the inclined plane at 30 degrees to the horizontal with a velocity 0.36 ms^-1. There is a cushion of fluid 1.8mm thick between the plate and plane. Find the viscosity of the fluid if the weight of the plate is 280N.
Homework Equations
viscosity = shear stress/velocity gradient
The Attempt at a Solution
shear stress = 280N / 0.6m^2 = 466.7 N/m^-2
converting 1.8mm to m gives 1.8 * 10^-3m
du = 0.36ms^-1
I'm not sure about how to go about dy, is the 1.8mm the length of the hypothenuse since its an inclined plane? If so does that mean dy becomes 1.8 * 10^-3m * cos 30. I'm sort of confused because it says 1.8mm thick, doesn't really tell if its the length of the hypotenuse. Thanks