Linus Pauling
- 187
- 0
1.
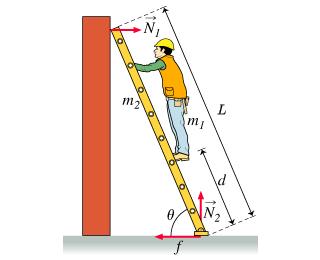
Suppose that the actual coefficent of friction is one and a half times as large as the value of . That is, . Under these circumstances, what is the magnitude of the force of friction that the floor applies to the ladder?
Express your answer in terms of , , , , , and . Remember to pay attention to the relation of force and .
2. static friction = magnitude of force in x direction, opposite sign
3. Ok, I had two exams today and I just almost went crazy calculating the the minimum friction force so that this ladder won't slip (brutal, but I did it). I am burnt out. How do I calculate N_1 here? It's the only force in the x direction other than friction, right? So by Newton's 2nd law the answer should just be friction = 1.5N_1, right?
Suppose that the actual coefficent of friction is one and a half times as large as the value of . That is, . Under these circumstances, what is the magnitude of the force of friction that the floor applies to the ladder?
Express your answer in terms of , , , , , and . Remember to pay attention to the relation of force and .
2. static friction = magnitude of force in x direction, opposite sign
3. Ok, I had two exams today and I just almost went crazy calculating the the minimum friction force so that this ladder won't slip (brutal, but I did it). I am burnt out. How do I calculate N_1 here? It's the only force in the x direction other than friction, right? So by Newton's 2nd law the answer should just be friction = 1.5N_1, right?